РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ЧЕРЕЗ МЕТАМАТЕРИАЛ ИЗ ЧЕРЕДУЮЩИХСЯ КИРАЛЬНЫХ СЛОЕВ
Журнал: Научный журнал «Студенческий форум» выпуск №2(225)
Рубрика: Физико-математические науки

Научный журнал «Студенческий форум» выпуск №2(225)
РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ЧЕРЕЗ МЕТАМАТЕРИАЛ ИЗ ЧЕРЕДУЮЩИХСЯ КИРАЛЬНЫХ СЛОЕВ
Киральность – в широком смысле слова это предмет, имеющий асимметрию со своим отражением. Это свойство, при котором объект не может совместиться со своим зеркальным двойником при каких-либо манипуляциях. Таким свойством обладают достаточно много предметов в нашей жизни, например, пропеллер самолета, спиральная нить или молекулы ДНК.
В истории много примеров проявления киральности в разных областях. В биохимии существуют примеры веществ идентичных по составу, но имеющих одно отличие – их молекулы зеркально отражены.
В оптике существуют естественные среды, имеющие свойства киральности, именуемые оптически-активными. Вторым случаем киральной среды в оптике являются холестерические жидкие кристаллы. Примером такого кристалла выступает эфир холестерина.
Также существуют искусственные среды, но для получения требуемых свойств неактивный материал необходимо поместить в магнитное поле.
В СВЧ-диапазоне могут существовать лишь искусственные среды, имеющие киральные свойства. Такая среда должна обладать пространственной дисперсией, для этого микроэлементы размещаются на определенном расстоянии, примерно равном длине волны излучения.
В таких средах могут использоваться трехмерные или двухмерные микроскопические элементы. При использовании трехмерных элементов среда называется объемной, в качестве микрообъектов используются спирали. Наряду с объемными моделями существует плоская двумерная структура, имеющая структуру в виде решетки, состоящая из полосковых S-образных элементов.
В настоящее время активно изучается искусственная киральная среда, так как такие среды обладают уникальными электродинамическими свойствами, позволяющими активно их применять для создания новых устройств. Новые возможности элементов в микроэлектронике открываются в электромагнитном поле, характеризующимся поляризацией. А с помощью киральных сред можно производить изменение вектора линейной поляризации электромагнитного поля.
Таким образом, можно сказать, что киральная среда – среда, создаваемая с помощью проводящих микрочастиц зеркально-ассиметричной формы.
В настоящее время активно изучаются свойства киральных метаматериалов, то есть структур с проводящими элементами зеркально асимметричной формы. В СВЧ-диапазоне могут существовать лишь искусственные среды, имеющие киральные свойства. Такая среда должна обладать пространственной дисперсией, для этого микроэлементы размещаются на определенном расстоянии, примерно равном длине волны излучения. В настоящее время активно изучаются различные структуры на основе киральных метаматериалов, так как такие среды обладают уникальными электродинамическими свойствами, позволяющими активно их применять для создания новых устройств.
В работе рассмотрено распространение электромагнитных волн СВЧ диапазона в периодически неоднородном волноводе из чередующихся планарных слоев с киральностью с различными значениями материальных параметров. У слоев изменяются как параметры киральности, так и диэлектрическая проницаемость. Геометрия задачи показана на рис. 1. В работе для описания киральных слоев использована модель Максвелла-Гарнетта. Для решения задачи использован метод частичных областей и теорема Флоке. Поле в периодически неоднородной структуре представляется в виде прямых и обратных гармоник Хартри. В результате решение задачи сводится к системе линейных алгебраических уравнений относительно неизвестных амплитудных коэффициентов волн, из которой получено дисперсионное уравнение для волн с право и левокруговыми поляризациями. Численный анализ показал, что в структуре волны с право и левокруговыми поляризациями обладают периодическими частотными окнами прозрачности и непрозрачности. В этом случае многослойный киральный метаматериал может выполнять роль частотно селективного фильтра для волн с право и левокруговыми поляризациями.
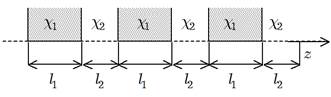
Рисунок 1. Геометрия задачи

