МОДИФИКАЦИЯ ПРОБЛЕМЫ КРУГА ГАУССА

MODIFICATION OF THE GAUSS CIRCLE PROBLEM

Vasily Perov

10th grade student of MBOU Secondary School No. 55, Russia, Irkutsk

Mikhail Perfilyev

Scientific adviser, Doctor of the International Academy of Natural Sciences, Russia, Irkutsk

Аннотация. Данная работа посвящена модификации проблемы круга Гаусса. Поставлена задача отыскания количества S(n) точек целочисленной решетки, лежащих на концентрических окружностях с центром в начале координат и радиусами, не превышающими . Показано, что отношение S(n)/n очень близко к числу Пи. Вычисления, сделанные в работе, реализованы на языке программирования Python.

Abstract. This paper is devoted to a modification of the Gauss circle problem. The task is to find the number of S(n) points of an integer lattice lying on concentric circles with their center at the origin and their radii not exceeding . It is shown that the ratio S(n)/n is very close to the number Pi. The calculations made in the work are implemented in the Python programming language.

Ключевые слова: проблема круга Гаусса, число Пи, язык программирования Python, целочисленные точки на окружности, целочисленная решетка.

Keywords: Gauss circle problem, number Pi, programming language Python, integer points on a circle, integer lattice.

Введение

Проблема круга Гаусса является задачей определения количества точек целочисленной решетки, которые попадают в круг заданного радиуса r с центром в начале координат [1]. Также эту задачу можно сформулировать так: какое количество пар целых чисел m и n удовлетворяют неравенству:

                                                           (1)

Если для заданного радиуса r обозначить значение количества таких точек как N(r), то получим последовательность N(r), где радиус  и является целым числом:

1, 5, 13, 29, 49, 81, 113, 149, 197, 253, 317, 377, 441, 529, 613, 709, 797, 901, 1009, 1129, 1257, 1373, 1517, 1653, 1793, 1961, 2121, 2289, 2453, 2629, 2821, 3001, 3209, 3409, 3625, 3853, 4053, 4293, 4513, 4777, 5025, 5261, 5525, 5789, 6077, 6361, 6625… [2]

При использовании функции округления вниз начение N(r) можно найти так:

 ,                                       (2)

где floor(x) — функция округления вниз.    

При использовании функции  (количество способов представить число n в виде суммы двух квадратов) можно записать:

 .                                                       (3)

Так как площадь круга радиуса r задается формулой , то может показаться, что число искомых точек целочисленной решетки будет равно примерно  , но в действительности истинное значение больше этого значения на некоторую поправку E(r) :

 .                                                     (4)

Проблема круга Гаусса как раз и состоит в отыскании верхней границы этой поправки, причем первые успехи в ее решении были сделаны выдающимся немецким математиком, физиком, механиком и астрономом Иоганном Карлом Фридрихом Гауссом. Согласно Гауссу [3]

 .                                                       (5)

Значительно позднее более точные оценки E(r) были получены другими математиками; также существуют обобщения проблемы Гаусса.

Модификация проблемы круга Гаусса

Известно, что количество точек целочисленной решетки, лежащих на окружности радиуса  с центром в начале координат, то есть удовлетворяющих равенству

 ,                                                           (6)

равно учетверенной разности между количеством натуральных делителей числа n, имеющих вид 4k+1, и количеством натуральных делителей, имеющих вид 4k+3.  [4]

Поставим задачу таким образом: найти количество целочисленных точек, лежащих на концентрических окружностях с центром в начале координат и радиусами, не превышающими , то есть удовлетворяющих уравнениям

 ,                                                          (7)

где  пробегает значения от 0 до n:  = 0;1;2;3;…;n.

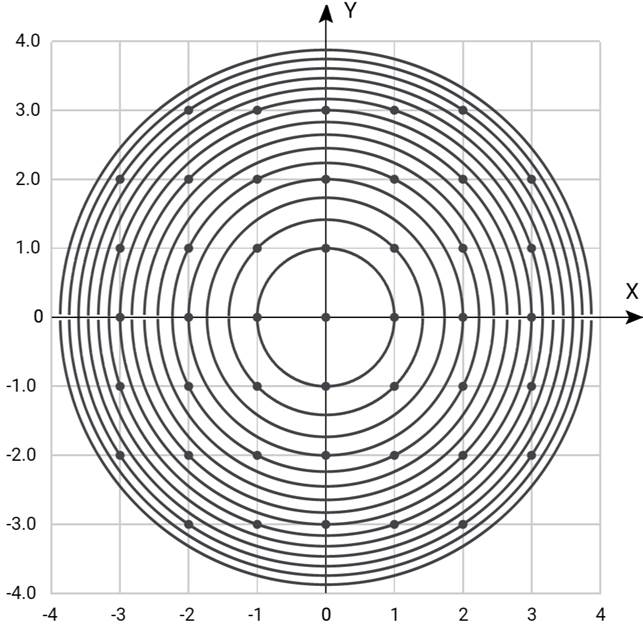
Рисунок 1. Точки с целыми координатами, лежащие на концентрических окружностях с центром в начале координат.

Обозначим искомое количество как S(n) и приведем программу расчета S(n) на языке программирования Python [5]. Условимся, что символ * означает отступ (space key).

s=0 #начальное значение суммы равно ноль

t=30000 #задаем значение t

for n in range(0,t+1): #n пробегает значения от 1 включая до t+1 не включая, то #есть до t включая

****l=0 #начальное количество делителей вида 4k+1 задаём нулевым

****m=0 #начальное количество делителей вида 4k+3 задаём нулевым

****k=0 #начальное значение k задаём нулевым

****while 4*k+1<=n: #до тех пор, пока 4k+1 не превысит n

********if n%(4*k+1)==0: #если n нацело делится на 4k+1

************l=l+1 #то увеличиваем l на 1

********k=k+1 #увеличиваем k на 1

****k=0 #снова обнуляем k

****while 4*k+3<=n: #до тех пор, пока 4k+3 не превысит n

********if n%(4*k+3)==0: #если n нацело делится на 4k+3

************m=m+1 #то увеличиваем m на 1

********k=k+1 #увеличиваем k на 1

****N=4*(l-m) #вычисляем количество целочисленных точек на одной #окружности

****s=s+N #добавляем это количество к общей сумме

print(s+1) #выводим искомую сумму на экран (учитывая точку с нулевыми #координатами)

Заметим, что отношение S(n)/n очень близко к числу Пифагора:

При n=100 получим S(n)=317; S(n)/n =3,17;

при n=500 получим S(n)=1581; S(n)/n=3,162;

при n=1000 получим S(n)=3149; S(n)/n=3,149;

при n=5000 получим S(n)=15705; S(n)/n=3,141;

при n=10000 получим S(n)=31417; S(n)/n=3,1417;

при n=20000 получим S(n)=62845; S(n)/n=3,14225.

Аналогичная программа на языке программирования C++ [7] :

#include <iostream>

using namespace std;

int main()

{int N,s,t,l,m,k,n;

s=0;

t=15;

for (n=0;n<=t;n++)

{l=0;m=0;k=0;

while (4*k+1<=n)

{if (n%(4*k+1)==0)

{l=l+1;}

k=k+1;}

k=0;

while (4*k+3<=n)

{if (n%(4*k+3)==0)

{m=m+1;}

k=k+1;}

N=4*(l-m);

s=s+N; }

cout<<s+1;

return 0;}

Заключение

Таким образом, в данной работе поставлена математическая проблема, похожая на проблему круга Гаусса. Суть проблемы заключается в отыскании количества точек с целыми координатами, которые лежат на концентрических окружностях с центром в начале координат и радиусами, не превышающими . Продемонстрирована компьютерная программа для быстрого расчета искомой величины S(n), показана связь частного S(n)/n с числом Пифагора.