МЕТОДЫ ГЛУБОКОГО ОБУЧЕНИЯ ДЛЯ КЛАССИФИКАЦИИ И ПРЕДСКАЗАНИЯ РАСПРОСТРАНЕНИЯ ВИРУСНЫХ ИНФЕКЦИЙ
Конференция: CLXX Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

CLXX Студенческая международная научно-практическая конференция «Молодежный научный форум»
МЕТОДЫ ГЛУБОКОГО ОБУЧЕНИЯ ДЛЯ КЛАССИФИКАЦИИ И ПРЕДСКАЗАНИЯ РАСПРОСТРАНЕНИЯ ВИРУСНЫХ ИНФЕКЦИЙ
С момента вспышки эпидемии в первые месяцы 2020 года распространение COVID-19 быстро росло в большинстве стран и регионов мира. В связи с этим Всемирная организация здравоохранения (ВОЗ) объявила SARS-CoV-2 чрезвычайной ситуацией в области общественного здравоохранения, имеющей международное значение. Вот почему ведутся активные работы над новыми методами, чтобы уменьшить дальнейший рост новых случаев и за счет разумного распределения пациентов уменьшить количество пациентов на одного врача, что может привести к более успешному лечению. Однако для надлежащего управления распространением COVID-19 необходимы модели прогнозирования в реальном времени, которые могут надежно поддерживать различные решения как на национальном, так и на международном уровне.
Проблема в разработке такой системы заключается в отсутствии общих знаний о том, как распространяется вирус и каково будет количество случаев заболевания каждый день. Текущие данные, доступные для исследований, имеют несколько недостатков, таких как ограниченные возможности тестирования и высокое непостоянство, несоответствия в отчетности (неполная отчетность), а общедоступные данные об уровне заражения в настоящее время ненадежны. Поэтому модель прогнозирования должна быть в состоянии сделать вывод о ситуации на основе прошлых данных таким образом, чтобы результаты отображали будущую тенденцию и были бы тесно связаны с реальными числами.
В истории есть несколько примеров, которые привели к тому, что люди узнали больше о природе инфекционных заболеваний, в том числе чума в 542 году н.э., унесшая миллионы жизней, и Черная смерть в 14 веке, которая была одной из первых известных зарегистрированных пандемий. Другой в этом списке была оспа, которая убила людей в количестве, превышающем число тех, кто участвовал в войнах в истории. Однако на сегодняшний день оспа является единственной болезнью, которую люди способны полностью искоренить. Холера, вспыхнувшая в девятнадцатом веке, остается проблемой и до сих пор не имеет полного излечения.
В то время как чума, черная смерть, оспа и холера затронули несколько миллионов человек, только во время пандемии в Уэнце в 1918 году люди пережили одно из величайших «стихийных бедствий» с точки зрения инфекционного заболевания двадцатого века с числом смертей, по оценкам, более 50 млн. В течение десятилетия после эпидемической модели Кермака-МакКендрика 1927 г. была введена модель возраста заражения, то есть модель, в которой заразность индивидуума зависит от времени, прошедшего с момента его заразности [1]. Это считалось одной из первых попыток сформулировать простую математическую модель для прогнозирования распространения инфекционного заболевания, в которой изучаемая популяция разделена на отсеки, а именно: потенциальный класс S, зараженный класс I и переболевший класс R. Простая модель эпидемии SIR может быть проиллюстрирована в виде частей, как показано на рисунке 1. Он не только был способен генерировать реалистичные единичные эпидемические вспышки, но и давал важные теоретические эпидемиологические выводы.

Рисунок 1. Модель отсеков в SIR
Здесь предполагается, что каждый класс находится ровно в одном отсеке и может перемещаться из одного отсека в другой. Динамика трех подгрупп S(t), I(t) и R(t) может быть описана моделью SIR, заданной связанными обыкновенными дифференциальными уравнениями (ОДУ) первого порядка [2].
Вдохновленный недавними разработками в области глубокого обучения, разработанный подход использует динамику инфекционных заболеваний и выводит интересующие скрытые величины (т. е. S, I и R) путем их аппроксимации с использованием глубоких нейронных сетей. Такой выбор мотивирован современными методами решения прямых и обратных задач, связанных с дифференциальными уравнениями, где искомое решение аппроксимируется либо нейронной сетью (рисунок 2), либо гауссовским процессом. В данном случае процесс автоматизирован.

Рисунок 2. Иллюстрация физически обученных нейронных сетей
Так как скорость распространения инфекции строго зависит от политики, ограничивающей социальное взаимодействие и поездки, то в работе моделируется рост числа случаев заболеваемости, используя данные о перемещениях, предоставленные Google (По требованию Роскомнадзора информируем, что иностранное лицо, владеющее информационными ресурсами Google является нарушителем законодательства Российской Федерации – прим. ред). Поскольку динамика населения различается, модели для конкретных регионов могут дать различные сведения и параметры. Данные о распространении инфекции по регионам также общедоступны в сети.
Чтобы оценить прогностическую способность любого алгоритма, он должен быть достаточно надежным, чтобы работать с данными, для которых параметры известны, а также с набором данных, для которых параметры неизвестны. Набор данных для известных параметров можно смоделировать, решив систему уравнений и добавив некоторый шум. Эффективность алгоритма может определяться тем, насколько хорошо он способен предсказывать истинные значения для широкого диапазона начальных предположений.
Для простоты вместо этого было сгенерированы данные путем решения систем обыкновенных дифференциальных уравнений с использованием алгоритма LSODA [3], начальных условий и истинных параметров, соответствующих каждому заболеванию (например, смертность) взяты из данных о заболеваемости. Чтобы сделать нейронную сеть информированной о болезни, после того, как данные были собраны, они вводятся в нейронную сеть без параметров. Стоит отметить, что в этой формулировке нет набора данных для обучения, проверки и тестирования, как в большинстве распространенных тренировок нейронных сетей, а только то, как болезнь распространяется во времени. Таким образом модель изучает системы и предсказывает параметры, которые их породили. Поскольку во многих из этих систем существует большой набор параметров, которые могут их генерировать, они были ограничены в определенном диапазоне вокруг истинного значения. Метод невероятно гибок в том смысле, что добавление, изменение или удаление ограничений можно выполнить с помощью одной простой строки кода.
Минимизирование потери среднеквадратичной ошибки осуществляется с помощью градиентного спуска. Градиентный спуск используется как метод нахождения минимального значения функции потерь. Функция используется, чтобы контролировать ошибку в прогнозах модели машинного обучения. Поиск минимума означает получение наименьшей возможной ошибки или повышение точности модели. Точность увеличивается, перебирая набор данных при настройке параметров нашей модели (весов и смещений).
Наконец, чтобы убедиться, что подход на самом деле так надежен, как кажется, было использовано 320 дней реальных данных. Нейронная сеть изучила совокупные случаи потенциальных, зараженных, умерших и выздоровевших и предсказала случаи на будущий месяц. В частности, из этих 320 дней сети были предоставлены данные за 280 дней, и она предсказала распространение на месяц в будущее. Сеть получила 31 точку данных (1 за 10 дней), была обучена на 100 тыс. эпох (примерно 5 минут), имела 9 слоев по 25 нейронов в каждом. Её вывод описан графиком на рисунке 3.
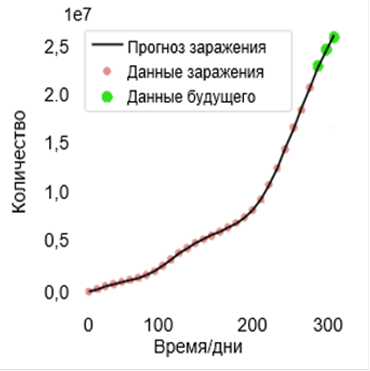
Рисунок 3. Результат предсказания нейронной сети
Результаты показывают, что обучаемые параметры, найденные в обеих сетях, немного отличались от изначальных. Это может означать, что-либо данные отличались от начального распределения данных, либо, это изменяющиеся во времени параметры, а не постоянные. Накопляющиеся случаи имели меньшую изменчивость данных и их было довольно легко изучить. Кроме того, удалось довольно точно предсказать будущий месяц. А вот ежедневные случаи имели гораздо больше вариаций данных и были более сложными.
В этой работе показан подход, который представляет собой нейронную сеть, способную изучать ряд заболеваний, способы их распространения, прогнозировать их прогрессирование и находить уникальные параметры, которые используются в моделях для описания динамики заболевания. Основываясь на простой модели SIR для COVID-19, можно смоделировать смертельные инфекционные заболевания. Демонстрируется простота, эффективность и универсальность этого подхода в соответствующих приложениях, в которых можно довольно легко обучать системы с небольшим количеством параметров и размерностей, а когда известны обучаемые параметры, время обучения может измениться с многих часов до нескольких минут. Результаты этой работы показывают, что физически обученная нейронная сеть является надежным подходом для создания характеристики и получения параметров, используемых в различных моделях для понимания динамики инфекционных заболеваний.





