Алгоритм оценки пульса с помощью камеры мобильного телефона

Думаем, что мы не ошибёмся, утверждая, что платформы для автоматического сбора информации с медицинских устройств и сохранение их в облачных хранилищах, в наши дни, становятся особенно популярными. Они обеспечивают доставку медицинских данных от устройства, которым обследуется пациент, в облачное хранилище.  Больной получает доступ к этой информации, не выходя из дома. А врач, может удалённо получать доступ к полной истории измерений, контролировать состояние пациента, давать рекомендации и вносить поправки в назначения. Не видя больного, он может определить, являются ли текущие показатели нормальными для данного пациента. И  всё это, почти полностью, автоматически. Одной из наиболее популярных платформ для сбора данных с медицинских устройств, является платформа - «MedM», компании «Swissmed Mobile».

Все алгоритмы для контактного подсчёта пульса, с помощью камеры мобильного телефона, которые существуют на данный момент, состоят из двух этапов. Первый – это преобразование кадра с камеры (рисунок 1), в какую-либо числовую характеристику. Второй – подсчёт и вычисление пульса, на основе зависимости данной числовой характеристики от времени.

На первом этапе, все алгоритмы работают, приблизительно, одинаково. На кадре выбирается область, и на ней считается числовая характеристика кадра. Затем, выбирается цветовая палитра и канал в этой области. Чаще всего используется цветовая палитра «RGB» с её красным каналом.  После этого подсчитывается среднее значение выбранного канала на выбранной, ранее,  области. В итоге, это среднее значение принимается за числовую характеристику данного кадра. Таким образом, алгоритм получает сигнал (рисунок 2), на котором можно чётко увидеть моменты притока крови к пальцу.

Задача второго этапа - по полученным данным определить пульс. На этом этапе можно выделить четыре основных класса алгоритмов:

•  Алгоритмы, основанные на подсчёте пиков [4].

•  Алгоритмы, основанные на подсчёте пиков с дополнительной логикой [5].

•  Алгоритмы, основанные на нахождении доминирующей частоты сигнала [2].

•  Алгоритмы, основанные на анализе спектра в плавающем окне [3][1].

Рисунок 1. Кадр с камеры с увеличенной контрастностью.

Рисунок 2. Пример сигнала,  после первого этапа, длиной 17 секунд

Алгоритмы, основанные на подсчёте пиков.

Этот класс алгоритмов опирается на простой подсчёт пиков, которые указывают на каждый приток крови. Производится он простым делением: количество найденных пиков на время измерения, таким образом, мы получает пульс. Но, у этого алгоритма есть небольшая проблема, это -  неустойчивость к ошибкам в детекции пиков. Т.е., пропуск одного или нескольких пиков приводит к значительному отклонению конечного результата. Например, пропуск двух пиков, при пульсе 60 уд/мин, при измерении длиной - 15 секунд,  приводит к тому, что алгоритм выдаст результат - 52 уд/мин, это сильно отличается от реального пульса.

Алгоритмы, основанные на подсчёте пиков с дополнительной логикой.

В основе этот класс алгоритмов лежит тот же, простой, подсчёт пиков. Но, эти алгоритмы пытаются исправить неточности первого класса. Они применяют  дополнительную логику при подсчёте пиков. Например: считая пики, алгоритмы с логикой, дополнительно вычисляют среднее расстояние между ними, и, если, через вычисленное среднее расстояние пик не обнаруживается, то к числу найденных пиков, просто добавляется единица. Так, частично, решается проблема пропуска пиков. Но проблема полной детекции пиков, данным типом алгоритмов, полностью не решена.

Например, на приведённом сигнале (рисунок 3), почти каждый пик, соответствующий притоку крови в палец, состоит ещё из двух пиков, которые, иногда, просто не отличаются друг от друга.  Это, во многих алгоритмах, может  привести к подсчёту лишних пиков.

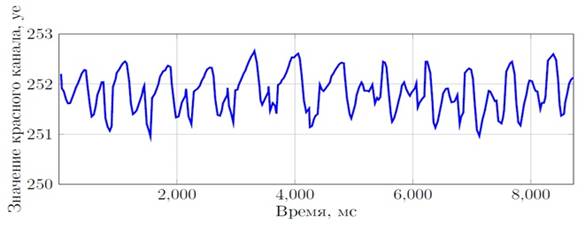
Рисунок 3. Пример проблемного сигнала

Алгоритмы, основанные на нахождении доминирующей частоты сигнала

Этот класс алгоритмов имеет совершенно другой подход к оценке пульса. Вместо нахождения отдельных пиков, алгоритмы рассматривают сигнал целиком и находят в нём доминирующую частоту. Доминирующая частота дискретного сигнала, как правило, находится при помощи  «дискретного преобразования Фурье» (ДПФ).  Оно позволяет получить зависимость амплитуды спектра сигнала от частоты. В этом случае, количество операций для получения спектра с помощью ДПФ равно О(N²), где N - количество отсчетов в исходном сигнале. Однако, используя алгоритм быстрого вычисления «дискретного преобразования Фурье (БПФ)», можно получать спектр дискретного сигнала за О(N*log(N)) операций, это позволяет применять данный алгоритм в режиме реального времени. После того, как производится расчет спектра сигнала, отбраковываются частоты, не соответствующие возможным значениям пульса человека. Из оставшегося диапазона частот выбирается частота с максимальной амплитудой.

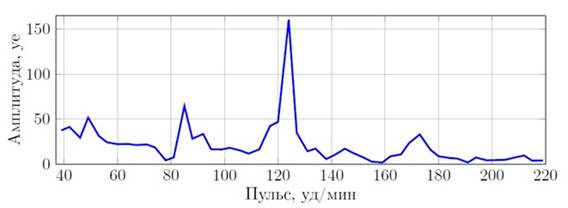
Рисунок 4. Пример участка спектра

Таким образом, получив такое разложение для всего измерения, достаточно найти частоту с самой большой амплитудой. Обязательно, перед этим нужно выбрать только те частоты, которым может соответствовать реальное значение пульса человека. Такие алгоритмы показывают измерения гораздо лучше, чем предыдущие два класса, и позволяют получать достаточно устойчивые результаты при длительной записи сигнала.

В данном алгоритме, так же, есть свои ограничения. При использовании БПФ размер входных данных должен быть степенью двойки и  дискретизация амплитудного спектра зависима от частоты и длины входных данных. Шаг дискретизации при измерении пульса вычисляется как – «60» *(частота/размер данных). Поэтому, для получения маленькой дискретизации, таким алгоритмам нужен большой размер входных данных. Например, для сигнала с частотой 30 и размером данных 1024, шаг дискретизации будет равен -  60*(30/1024)»1.76. Поэтому, чтобы получить такую дискретизацию, входной сигнал должен иметь длину 1024/30»34 секунды.

Алгоритмы, основанные на анализе спектра в плавающем окне.

Алгоритмы, описанные выше, имеют один, довольно таки существенный, недостаток. При небольшой выборке по времени, они очень чувствительны к шуму, который имеет высокую амплитуду и расположен в небольшой части сигнала. На примере  приведённого сигнала (рисунок 5) можно заметить, что первые шесть секунд измерения занимает шум, к тому же, он имеет высокую амплитуду. Это может привести к тому, что итоговый спектр получит ложный пик на частоте данного шума, который также будет иметь наибольшую амплитуду.  Итог - неправильный результат. Поэтому, исходный сигнал предварительно разбивается на пересекающиеся отрезки. Дальнейшие действия зависят от алгоритма. Чаще всего, разделение на пересекающиеся отрезки используется для того, чтобы отбросить части сигнала, которые выбиваются из общего спектра. Например, если доминирующая частота на каком-то отрезке отличается от остальных, то данный отрезок просто отбрасывается. Можно заметить, что при разбиении на отрезки, происходит уменьшение размера входных данных для БПФ. Следовательно, размер шага дискретизации будет увеличиваться. Таким образом, результат, полученный исключительно за счёт вычисления БПФ для отрезков, будет иметь крайне маленькую точность по сравнению с ответом, полученным после вычисления БПФ для всего измерения.

Рисунок 5. Пример сигнала с шумом с высокой амплитудой