МЕТОДИКА СОСТАВЛЕНИЯ УРАВНЕНИЙ 4-ОЙ СТЕПЕНИ С ПАРАМЕТРОМ

В данной работе рассматривается метод моделирования уравнений 4-ой степени относительно переменной  и как квадратное относительно параметра.

Уравнения такого типа появлялись на вступительных экзаменах уже в 70-ые годы прошлого века [1, с. 26]. Данная статья направлена на популяризацию задач с параметрами среди школьников, студентов и учителей.

Задачи с параметрами на ЕГЭ профильного уровня решают на 4/4 баллов в среднем 3-4% школьников. К сожалению, около 90% школьников даже не приступают к решению данной задачи. Кроме этого, существует еще одна значимая проблема: для учителей и учеников по некоторым типам задач бывает просто-напросто недостаточно вариантов, предложенных в дидактических материалах. Поэтому в данной статье представим методику составления вышеуказанных уравнений. Эту задачу может осилить большинство учеников 8 класса, которые умеют решать квадратные уравнения.

Действительно, главная идея состоит в том, что, если квадратное уравнение имеет корни  и , то это уравнение можем записать в виде:

или по теореме Виета: .

Суть составления таких уравнений: берем два квадратных трехчлена  и , составляем квадратное уравнение относительно параметра .

                                                                                             (1)

Очевидно, корнями квадратного уравнения относительно параметра  будут  и , а это уравнение фактически равносильно совокупности двух квадратных уравнений с параметром . Следовательно объединение решения двух квадратных уравнений относительно , будет решением исходного уравнения 4-ой степени.

Давайте реализуем алгоритм на конкретном примере.

Пусть  и .

Тогда, уравнение (1) примет вид: 

Раскрыв скобки, получим:

Давайте решим полученное уравнение относительно  как квадратное уравнение.

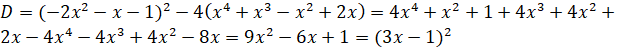
Очевидно, мы получили:

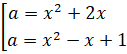
Итак, наше уравнение свелось к решению совокупности двух квадратных уравнений с параметрами, о которых говорили выше.

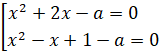
Начнем с решения первого уравнения:

1)         , , 

2)         , , 

3)         , , 

Нет действительных корней

Рассмотрим второе уравнение:

1)         , , 

2)         , , 

3)         , , 

Нет действительных корней

Давайте объединим полученные результаты в таблицу:

Таблица 1.

Количество решений в зависимости от значения параметра

Ответ: при  , нет действительный корней

при  , 

при  ,  , 

при  ,  ,  , 

при  ,  , ,

  ,   

Мы рассмотрели уравнения, корни которого при решении как квадратного уравнения относительно параметра  – квадратные трехчлены. Для решения таких уравнений достаточно уметь решать квадратные уравнения с параметром, например,  [2, с. 143]. Подобные уравнения встречаются в учебниках 8 класса.

Таким образом, мы получили простой способ составления уравнений 4-ой степени относительно  с параметром , которые сводятся к совокупности двух квадратных уравнений с параметром. Учитель, взяв любые два квадратных трехчлена, может составить аналогичные уравнения, тем самым, становится возможным составление множества задач, необходимых для закрепления пройденного материала.