Анализ методик ускоренной оценки старения изоляции электрооборудования

Введение

Старение изоляции электрооборудования функционально зависит от режима эксплуатации в условиях воздействия комплекса внешних факторов.  Системное воздействие комплекса факторов результирующего воздействия может существенно снизить остаточный ресурс электрооборудования [Коржов,2016; Полищук, 2017]. В то же время при пониженном износе изоляции, связанным, например, с воздействием благоприятного термического режима, реальный срок службы возрастает и оказывается возможным обойтись не заменой изоляции по истечении срока службы, а ее чисткой, пропиткой и сушкой. Это становится особенно актуальным в связи с тем, что значительная доля в общем распределении количества используемого электрооборудования эксплуатируется вблизи или за пределами расчетного срока службы. С точки зрения практики и экономической потребности в оценке старения изоляции, возникающей при ее эксплуатации, повышается актуальность в данных о реальном остаточном ресурсе электрооборудования и вероятностях  выхода его из строя.

Существующие методы оценок старения изоляции оборудования

С экономической точки зрения необходимым условием работы  различных комплексов оборудования, работающих в различных отраслях промышленности является надежность изоляции электрооборудования. Практически всем дефектам в изоляции присуща определенная скрытность, а  локализация такого повреждения представляет собой весьма нетривиальную задачу. Классические методы оценки разрушения изоляции электрооборудования, основаны на концепциях термического старения, водных и электрических пробоях -  триингах при эксплуатации в присутствии воды и под воздействием электрического напряжения [Васин, 2008]. 

Например,  динамику теплового износа обмоток трансформатора можно оценить используя интегральное представление Монтзингера:

                                                                                                        (1),

где  Т - срок службы,    - температура наиболее нагретой точки обмотки трансформатора, Δ — постоянная температура, принимаемая равной 7 ºC. Подынтегральная  экспоненциальная функция отражает скорость старения изоляции. Наиболее нагретые зоны, из которых согласно соотношению необходимо отобрать образцы бумажной изоляции локализуются в удаленных местах. Следствием этого является то, что, как правило, пробы отбираются из доступных мест.  Разработанные методы по оценке температуры в наиболее нагретой области дают весьма близкие результаты с учетом особенностей конструкции, данных о нагрузке, температуре окружающей среды  и т. д., но только при наличии исходных данных за весь период эксплуатации трансформатора. При отсутствии таких данных ошибка расчета интеграла выражения 1 весьма существенна.

Интересным представляется разработка устройств для отслеживания срока службы по данным измерений температуры в каждый отдельный интервал времени [Серебряков, 2014]. На старение в сильной степени влияют и другие факторы, которые могут снизить срок службы в десятки раз. Для учета  окисления масла или  водного трииинга можно воспользоваться следующим выражением:

                                                                                                     (2)

В выражении  (2) g(x) представляет собой результирующую функцию, отражающую либо влияние окисления масла,  либо водного трииинга. Здесь стоит учитывать, что во многих случаях внутренние слои изоляции, прилегающие к проводнику, оказываются менее состаренными, чем внешние слои, напрямую контактирующие с маслом. Как показывают расчеты в [Васин, 2008] совместный учет увлажнения бумаги и окисления масла может привести к увеличению скорости старения изоляции в десятки раз. Помимо  влияния степени окисления масла и водного трииинга модификация формулы Монтзингера может описывать влияние и других факторов, например, содержание кислорода [Конограй, 2010],  природных сернистых соединений в масле [Вилданов, 2013].

На существующие методы оценки изоляции в лаборатории затрачивается большое количество времени. Существенные временные затраты связаны с отбором изоляции и методами дальнейшей оценкой растворенных фурановых соединений в масле  и полимеризации бумаги  в химической лаборатории; исследования прочности на излом при многократных перегибах. Для уменьшения временных затрат существует метод основанный на линейной зависимости степени полимеризации от коэффициента отражения электромагнитных волн с длиной волны λ = 650 нм от трансформаторной бумаги [Козлов, 2015].

Обсуждение перспективных методов оценки старения изоляции электрооборудования

В разработке метода ускоренной оценки старения изоляции электрооборудования  перспективным представляется направление математического моделирования состояния  изоляции электрооборудования в части учета минимального набора неизвестных параметров. Развитый сегодня математический аппарат позволяет разрабатывать математические модели изоляции электрооборудования, в том числе, построенные на теории вероятностей и математической статистке. В части достижения цели настоящей работы, связанной с разработкой основ метода оценки старения изоляции, прежде всего, определим те условия, учет которых позволит выполнить статистико-вероятностные оценки старения изоляции. 

Предварительный этап построения модели старения  изоляции  должен включать в себя выбор входных и выходных параметров, а также сбор и предварительную обработку результатов лабораторных и производственных испытаний в соответствии с требованиями, налагаемыми типом модели. Очевидно, что модель старения  изоляции должна быть основана на анализе временных  состояний изоляции  с учетом действия факторов окружающей среды и режимов работы, а также реалистичности динамики некоторого интегрального диагностического параметра, с помощью которого возможно описать состояние изоляции под действием множества факторов. 

В настоящей работе  оценку времени старения изоляции предлагается выполнять на основе учета деформаций формы распределения функции вероятности повторяемости диагностического параметра, в качестве которого могут выступать, например, либо твердость изоляции, либо прочность, либо степень полимеризации бумаги. Как уже указывалось, на качество бумажной изоляции трансформаторов большое влияние оказывают множество факторов. Одним из вариантов решения задачи по объективному определению времени старения бумажной изоляции  является единовременный учет нескольких факторов. А именно, интегральное модифицированное представление Монтзингера будет иметь вид:  

       ,

где K,    - текущий и базовый показатель кислотности масла,  W,    - текущий и базовый показатель влагосодержания изоляции, N,   - содержание кислорода,  – отражающая содержание  природных сернистых соединений в масле, ni – показатель степени для фактора.

Для решения задачи по определению старения изоляции оборудования, включая не только трансформаторы, но и кабели далее мы будем рассматривать схему построения модели старения на основе рассмотрения величины твердости кабельных изоляции оборудования методами математической статистики. Оценка степени диалектрического старения реализуется путем измерения твердости (HSA) материала изоляции по методу Шора.  Как показано, в работе [Власов, 2015] можно считать, что распределение вероятности повторяемости твердости с высокой точностью  подчиняется нормальному закону.  С этой точки зрения оценка времени старения изоляции предусматривает накопление некоторого массива данных. Причем каждое значение из полученной выборки (массива) твердостей представляет собой случайную величину, принимающую значение, заключенную в некоторых пределах. Многие аспекты случайного процесса практически полностью исписываются функцией плотности вероятностей, характеризующей  вероятность попадания случайной величины в заданный интервал.

В частности, одним из наиболее распространенных законов является Гауссово распределение плотности вероятности, имеющее следующий вид:

                                               ,

где   - среднее квадратичное отклонение,  - среднее значение твердости изоляции.

Так, результаты исследований твердости изоляции, выполненные в работе [Власов, 2015] показывают, что для экспресс-оценки качества изоляционного материала могут быть использованы  функций распределения твердости. В настоящей работе в качестве характеристик изоляционного материала предлагается применять не просто функцию распределения F(H) или оценки моментов распределения, а деформации формы функции плотности вероятности повторяемости f(H), отражающую значение вероятностной меры в конкретном  элементе множества.

Таким образом, в качестве основы настоящего исследования предлагается использовать оценки деформаций формы распределения функции вероятности повторяемости. В частности, известно, что по мере старения изоляции значения твердости при формировании выборки будут повышаться [Агарков,2016]. Следовательно, будет возрастать и среднее значение твердости. Анализ нормального распределения показывает, что это приведет к смещению центра и всего распределения вдоль оси абсцисс вправо.  Следовательно, можно ожидать три возможных случая: исходного распределения соответствующего не  состаренной изоляции, случая состаренной изоляции и промежуточного некоторого работоспособного состояния.

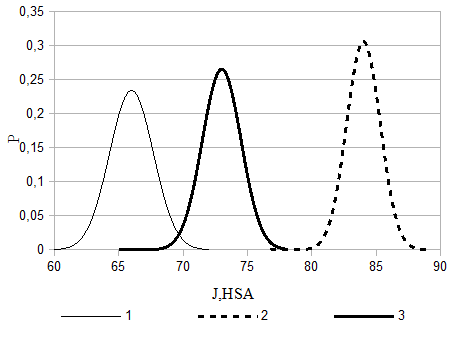
Рисунок 1.  Кривые нормального (Гауссова) распределения плотности вероятности для трех случаев, полученные по данным оцифровки функций распределения, представленных в работе [Власов, 2015]:  1 -  исходное распределение твердости изоляции,  3 -  распределение твердости разрушающейся изоляции, 2 -   промежуточное состояние

На рис.1 условно показаны кривые нормального (Гауссова) распределения для трех случаев, полученные по данным оцифровки функций распределения, представленных в работе [Власов, 2015]. Анализ данных работы [Власов, 2015] позволяет заключить, что для изоляции возможны, по крайней мере, три случая: 1 - когда распределение соответствует исходному состоянию, 3 – когда,   распределение соответствует, например, пробоям изоляции, и 2 – промежуточное состояния разрушающегося, но рабочего изоляционного покрытия. На рис.1 непрерывной тонкой кривой, обозначенной цифрой 1, показано исходное распределение твердости изоляции. Пунктирной кривой, обозначенной цифрой 3, показано  распределение твердости разрушающейся изоляции. Цифрой два обозначена кривая нормального распределения для  промежуточного состояния.

Таким образом, рассматривая семейство функции плотности вероятности в их динамике, можно по смещению моды функции и изменению ее амплитуды за счет вариаций среднего квадратического отклонения  можно составить номограммы для определения старения изоляции.

Как показывают экспериментальные данные  функции  плотности распределений механических характеристик изоляции могут отличаться от формы, предсказываемой моделью Гаусса [Лицкевич, 2015].  Например, функция плотности распределения ресурса промасленной изоляции силового кабеля [Лицкевич, 2015] отличается от нормального закона.    В этом  случае для ее описания можно предложить  использовать  подстраиваемую выбором параметров  и  функцию плотности вероятности, описываемую бета-распределением:

                           ,

где, B — бета функция с произвольными фиксированными параметрами  , величины A и C  - некоторые базовые значения твердости. 

Средневзвешенное значение соответственно имеет вид:

,

где  - соответственно оптимистическая  наиболее вероятная  и пессимистическая оценки. По данным выборки задавая форму функции распределения  в виде бета-распределения оказывается возможным получить значения  оптимистической,  наиболее вероятной  и пессимистической оценок допустимой твердости изоляции. Функция распределения плотности вероятности, устанавливающую связь между случайной величиной и вероятностью ее появления,  дает возможность определить с той или иной долей вероятности (надежности)  допустимую работоспособную твердость изоляции. Зная же форму функции распределения и ее деформации в динамике,  возможно, определить время старения изоляции.

Заключение

В качестве основы экспресс способа определения старения изоляции электрооборудования предложено учитывать деформации функции плотности распределения твердости изоляции,  устанавливающей связь между случайной величиной и вероятностью ее появления. Анализируя семейство функции плотности вероятности в части перехода формы от номинальной, соответствующей исходному (не состаренному состоянии изоляции)   к наиболее измененной функции распределения по смещению моды функции и изменению ее амплитуды за счет вариаций среднего квадратического отклонения возможно составить номограммы для определения старения изоляции в  их динамике.  Эти номограммы по вероятностным характеристикам на конкретных примерах позволят определять  состояние изоляции при котором возможно существенное сокращение срока службы оборудования,  а также с определенной вероятностью  выявлять остаточный ресурс, степень старения изоляции относительно предельно допустимому уровню и области с аномальным старением.