ИНТЕГРАЛЬНАЯ ОЦЕНКА ПАРАМЕТРОВ ДВИЖЕНИЯ ВОЗДУШНОГО СУДНА

INTEGRAL ESTIMATION OF AIRCRAFT MOVEMENT PARAMETERS

Alexander Kodrin

Student, St. Petersburg State University of Civil Aviation,  Russia, St. Petersburg

Anton Alimov

Student, St. Petersburg State University of Civil Aviation, Russia, St. Petersburg

Oksana Kareva

Student, St. Petersburg State University of Civil Aviation, Russia, St. Petersburg

Loznitsa Stefan

Senior lecturer, St. Petersburg State University of Civil Aviation, Russia, St. Petersburg

Аннотация. В статье рассмотрено применение интегрирования для оценки параметров движения воздушного судна.

Abstract. The article considers the application of integration to assess the parameters of aircraft movement.

Ключевые слова: интеграл, воздушное судно, параметры движения

Keywords: integral, aircraft, motion parameters

Интеграл (от лат. integer — «целый») — одно из важнейших понятий математического анализа, которое возникает при решении задач:

• о нахождении площади под кривой;
• пройденного пути при неравномерном движении;
• массы неоднородного тела и т. п.;
• а также в задаче о восстановлении функции по её производной (неопределённый интеграл).

Интеграл используется и в других науках, таких как физика, биология, экономика.

В авиационной отрасли интеграл также находит свое применение:

• в аэронавигации: для расчета высоты самолета по его скорости и времени; определения расстояния, пройденного самолетом, на основе его скорости; определения тяги; расчета траекторий полета ЛА; расчета других параметров, таких как угол наклона самолета, сила тяги двигателя и т. д.;
• в метеорологии: для определения температуры на основе данных о скорости ветра, влажности воздуха и других параметрах; расчета высоты облаков, скорости и направления ветра и других параметров, которые важны для обеспечения безопасности полетов;
• в аэродинамике: для вычисления подъемной силы, сопротивления и моментов, действующих на самолет.

В качестве примеров приведем расчеты барограммы набора высоты, дальности набора высоты, дальности и продолжительности горизонтального полета, дальности снижения с помощью интеграла.

Расчет минимального времени набора заданной высоты сводится к определению интеграла:

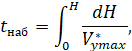
Где V*_ymax – максимальная вертикальная скорость на каждой принятой высоте.

При заданной высоте H₀ продолжительность набора t_наб находится по построенной барограмме, используя предыдущую формулу. Тогда дальность набора высоты можно свести к нахождению интеграла:

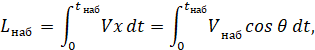
где

θ – угол наклона траектории.

В общем случае дальность и продолжительность горизонтального полёта определяют по формулам:

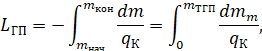
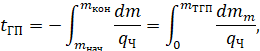
где

q_ч – часовой расход топлива, [кг/ч];

q_K – километровый расход топлива, [кг/км];

m_нач, m_кон – масса воздушного судна в начале и в конце горизонтального полёта на крейсерском

режиме, [кг];

m_ТГП ≈ (m_нач - m_кон) - запас топлива, который может быть израсходован в горизонтальном полёте, [кг]

Расчет дальности и продолжительности планирования производится, основываясь на предположении, что планирование имеет место под наивыгоднейшим углом атаки α_наив В этих условиях в общем случае дальность планирования определяется как:

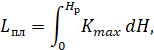
где

K_max – максимальное аэродинамическое качество,

H_р – расчетная высота.

Практическое применение интегрирования в авиации можно рассмотреть на примере расчета студентом дальности планирования учебного самолета Dimond DA40 NG с отказавшем двигателем, при выполнении учебного полета по кругу. Максимальное аэродинамическое качество данного самолета K_max = 9,4. Истинная высота полета по кругу составляет 1100 футов, что примерно равно 335 м. Таким образом, получаем выражение:

 = 3149 м

Теоретически, самолет сможет долететь до торца полосы, если отказ двигателя произошел на удалении менее 3149 м.

Таким образом, интеграл – это важный «инструмент» математики, применяемый в самых разных областях науки и техники.