РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ КИНЕМАТИКИ В УПРАВЛЕНИИ КОНЕЧНОСТЯМИ ЧЕТВЕРОНОГОГО РОБОТА

В статье предложено математическое решение расчета обратной задачи кинематики для конечности четвероногого робота. Решение предложено с помощью тригонометрический формул для простого понимания и расчета при проектировании системы управления.

В конечность четвероногого робота имеет всего 3 степени свободы, поэтому нет необходимости более сложных алгоритмов на примере Денавита-Хартенберга.

Решение задачи кинематики позволяет определить целевые углы положений звеньев конечности, зная координаты точки в пространстве. Для правильного расчета необходимо знать длины от каждых звеньев конечности робота в цепочке. На рисунке 1 представлена модель четвероногого робота, для которого будут производиться расчеты.

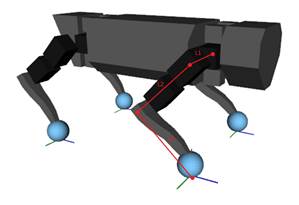
Рисунок 1. Модель четвероногого робота

При создании модели кинематики конечности робота имеются следующие данные:

- L1 - длина первого звена конечности четвероногого робота и показана на рисунках 2-4 , как отрезок ОА;

- L2 - длина второго звена ноги четвероногого робота и обозначается на рисунках 2-4, как отрезок AB;

- L3 - длина третьего звена ноги четвероногого робота и обозначается на рисунках 2-4, как отрезок BC;

- размер dx - описывает расстояние смещения конечности робота по оси оX

- размер dy - описывает расстояние смещения конечности робота по оси оY

- размер dz - описывает расстояние смещения конечности робота по оси оZ

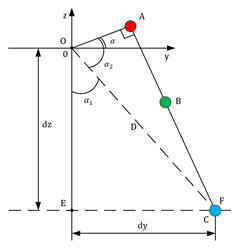
Рисунок 2. Схема кинематики конечности вид сзади

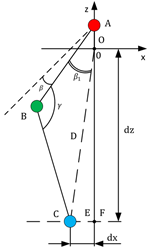
Рисунок 3. Схема кинематики конечности вид сбоку

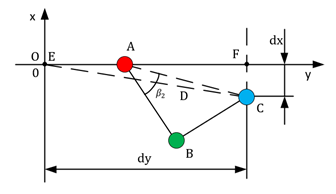
Риснуок 4. Схема кинематики конечности вид сверху

Первый этап. Нахождение угла .

Значения угла  используется для определения положения первого сервопривода в цепи звеньев ноги робота, то есть угла поворота оси сервопривода относительно его нулевого положения.

Угол  расчитывается, как разница углов  и . Найдем длину главной диагонали D по формуле (1).

                                                                                                   (1)

Рассмотрим треугольник AOB, где AO = L₁, который является прямоугольным, смотря по конструкции ноги робота, и находим угол  по формуле 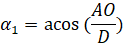(2).

                                                                                                           (2)

Для нахождения второго вспомогательного угла  расмотрим треугольник EOF, где EF = dy, OE = dz, который также является прямоугольным и по т. Пифагора найдем его диагональ по формуле (3).

                                                                                                        (3)

Зная все необходимые длины треугольника, найдем угол  по формуле 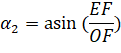(4).

                                                                                                              (4)

Найдя два вспомогательных угла, можем вычислить угол  по формуле (5).

                                                                                                                 (5)

Второй этап. Нахождение угла .

Значения угла  используется для определения положения второго сервопривода в цепи звеньев ноги робота, то есть угла поворота оси сервопривода относительно его нулевого положения.

Угол  расчитывается, как разница углов  и .

Рассмотрим треугольник EOC, который является прямоугольным, EC = dx, OE = dz, и найдем угол  по формуле (6).

                                                                                                            (6)

Рассмотрим треугольник AOC, который является прямоугольным, AO = L₁, OC = D и найдем его диагональ по формуле (7).

                                                                                                        (7)

Рассмотрим треугольник ABC. Зная три длины треугольника, AB = L₂, BC = L₃ по т. косинуса найдем угол  по формуле 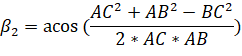(8).

                                                                                            (8)

Найдя два вспомогательных угла, можем вычислить угол  по формуле (9).

                                                                                                             (9)

Третий этап. Нахождение угла .

Значения угла  используется для определения положения третьего сервопривода в цепи звеньев ноги робота, то есть угла поворота оси сервопривода относительно его нулевого положения.

Для его нахождения рассмотрим треугольник ABC, в котором ранее были посчитаны все длины сторон треугольника, поэтому по т. косинуса вычислим значение угла по формуле 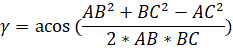(10):

                                                                                                (10)

В данном разделе была представлена математическая модель решения задачи обратной кинематики для четырех робота, а также описаны методы ее решения и использования тригонометрических формул. Решение задачи обратной кинематики является важным шагом в создании управляемых роботов и позволяет точно определить необходимые углы и координаты для достижения заданной конечной точки. Предложенные методы решения, основанные на геометрических и тригонометрических принципах, являются эффективными и могут быть применены как для четырехногих, так и для других типов роботов, использующие похожую кинематику движения.