КОМБИНИРОВАННЫЙ ПОДХОД ДЛЯ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ КИНЕМАТИКИ МАНИПУЛЯТОРОВ С ИЗБЫТОЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ ПОДВИЖНОСТИ

PARTICLE SWARM OPTIMIZATION METHOD FOR SOLVING THE REDUNDANT MANIPULATORS INVERSE KINEMATICS

Akhmed Dzhachaev

Student, Moscow State Technical University them N. E. Bauman, Russia, Moscow

Аннотация. В статье рассматривается применение алгоритмического решения обратной задачи кинематики манипулятора с избыточным числом степеней подвижности, основанного на комбинированном подходе, который сочетает метод роя частиц и метод Левенберга-Марквардта. Показано, что в рамках поиска оптимальной конфигурации манипулятора данный подход позволяет минимизировать ошибку позиционирования схвата, компенсируя слабые стороны каждого из алгоритмов в отдельности. Проведено моделирование работы алгоритма для ряда тестовых задач в условиях различных начальных конфигураций манипулятора и целевых позиций и определена эффективность предложенного подхода.

Abstract. The paper discusses an algorithmic solution to the inverse kinematics problem for a manipulator with redundant degrees of freedom, based on a hybrid approach that combines Particle Swarm Optimization and the Levenberg–Marquardt method. The proposed method effectively minimizes the end-effector positioning error when searching for an optimal manipulator configuration, leveraging the strengths and compensating for the weaknesses of each individual algorithm. The algorithm's performance is evaluated through simulation on a set of benchmark tasks involving various initial manipulator configurations and target positions. The results demonstrate the efficiency of the proposed approach.

Ключевые слова: система управления манипулятором, обратная задача кинематики, метод роя частиц, метод Левенберга-Марквардта, методы оптимизации, избыточные степени подвижности, комбинированный подход.

Keywords: Manipulator control system, inverse kinematics problem, particle swarm optimization, Levenberg–Marquardt method, optimization methods, excessive number of degrees of freedom, hybrid approach.

Введение

В настоящее время роботы-манипуляторы широко применяются в различных отраслях промышленности и сферах услуг. Среди множества задач существуют такие, где особое значение имеет достижение манипулятором нужной рабочей зоны с учетом пространственных ограничений, возникающих в конкретных условиях эксплуатации. Это обусловило появление специализированных типов манипуляторов, способных удовлетворить данные требования, главным образом, манипуляторов с избыточным числом степеней подвижности (МИСП). Благодаря наличию дополнительных степеней подвижности МИСП способны эффективно позиционировать рабочий инструмент по положению и ориентации в труднодоступных зонах рабочей области, обусловленных спецификой технологических операций [1]. Например, при сварке такой спецификой может выступать сложная форма свариваемых деталей. На рис. 1 показано преимущество 7-степенного робота-манипулятора (рис. 1, б) перед обычным 6-степенным роботом-манипулятором (рис. 1, а) – наличие дополнительной степени подвижности позволяет обрабатывать весь периметр сварного шва [2].

а                                                                                  б

Рисунок 1. Демонстрация сварочной операции: а – 6-степенного робота-манипулятора, б – 7-степенного робота-манипулятора

Однако увеличение степеней подвижности приводит к усложнению задачи разработки системы управления манипулятором, в частности, это касается решения обратной задачи кинематики (ОЗК). ОЗК заключается в определении набора обобщенных координат звеньев манипулятора, исходя из заданных значений положения и ориентации его схвата [3] (рис. 2, а). В противоположность этому, прямая задача кинематики (ПЗК) сводится к расчету положения и ориентации схвата на основе известных значений обобщенных координат (рис. 2, б).

   
а                                                                      б

Рисунок 2.  Две задачи кинематики манипулятора: а – обратная (ОЗК) и б – прямая (ПЗК)

Для манипуляторов с избыточным числом степеней подвижности характерна ситуация, при которой количество степеней подвижности превышает число пространственных степеней свободы схвата. Подобная избыточность увеличивает доступную рабочую зону манипулятора, однако одновременно порождает множественность допустимых решений, ограничивая таким образом выбор подходящих методов решения ОЗК [4].

Так, традиционные аналитические методы решения ОЗК предполагают выведение явных математических зависимостей для обобщенных координат звеньев манипулятора, однако их применение ограничено относительно простыми системами с небольшим числом степеней подвижности [5]. В случае манипуляторов с избыточными степенями подвижности аналитические подходы становятся практически непригодными из-за высокой сложности вывода соответствующих уравнений, вызванной наличием множества возможных решений [6]. Кроме того, аналитические методы не позволяют эффективно учитывать дополнительные оптимизационные критерии, например, предотвращение коллизий [7].

Численные методы, такие как алгоритм градиентного спуска и метод Ньютона, часто применяются для поиска решений в многомерном пространстве [8]. Однако они также имеют свои недостатки. Во-первых, эти методы существенно зависят от выбора начальной точки, что может привести к попаданию алгоритма в локальный оптимум [9]. Во-вторых, вычислительная сложность таких методов возрастает экспоненциально при увеличении размерности задачи, что заметно снижает их практическую применимость в случае манипуляторов с избыточными степенями подвижности [10].

Выбор оптимального метода решения ОЗК становится особенно актуальным при функционировании манипулятора в динамично изменяющейся рабочей среде, поскольку неопределенность рабочей области требует от системы управления непрерывного проведения вычислительных операций в режиме реального времени для своевременного нахождения актуального решения ОЗК [11]. В качестве целевого примера рассмотрим 7-ми осевой МИСП KUKA iiwa 14 R820, ассистирующий человеку при выполнении сборочно-монтажных операций (рис. 4) [12].

Рисунок 4. Совместное выполнение сборочно-монтажных операций с помощью МИСП

Как следует из рис. 4, в рабочей области МИСП присутствует ряд динамичных объектов, что требует при поиске оптимальной конфигурации манипулятора учесть еще один критерий – отсутствие коллизий, где под коллизиями понимается столкновение с объектами окружающего пространства. Геометрия данных объектов выступает дополнительным фактором, формирующим пространство поиска возможных решений ОЗК.

Таким образом, указанные выше особенности требуют разработки альтернативных подходов, способных эффективно решать задачи многокритериальной оптимизации при управлении манипуляторами с избыточным числом степеней подвижности. Данный вопрос уже рассматривался в нескольких исследованиях, где авторами было предложено применение нейросетевых и эвристических методов оптимизации для улучшения эффективности решения ОЗК [13-15]. Однако в этих работах не уделялось достаточного внимания учёту возможности возникновения коллизий при движении манипулятора. Помимо этого, используемые методы характеризуются значительным снижением вычислительной эффективности по мере увеличения размерности пространства поиска, а также неспособностью гарантированно обеспечить достижение глобального оптимума в ряде задач [16-17].

В данной работе в качестве альтернативного подхода предлагается использовать комбинированный подход, основанный на сочетании метода роя частиц (Particle Swarm Optimization, PSO), основанного на применении роевого интеллекта и имитирующего поведение природных популяций, и метода Левенберга-Маркварда (Levenberg-Marquardt, LM), одно из широко распространенных методов оптимизации [18]. Оба этих метода уже получили применение в различных прикладных научных областях, включая робототехнику [19].

Постановка оптимизационной задачи

Чтобы лучше понять предложенный алгоритмический подход, рассмотрим ОЗК как оптимизационную задачу. Для наглядности возьмём в качестве примера 2-звенный манипулятор, схват которого необходимо переместить в целевую точку (рис. 5). Помимо манипулятора, в рабочей области также присутствует препятствие, столкновение с которым нужно избежать.

Рисунок 5. Иллюстрация постановки оптимизационной задачи в рамках решения ОЗК

В данном случае элементами математического пространства поиска являются векторы , состоящие из обобщенных координат манипулятора . Каждому вектору  соответствует некоторое значение целевой функции , которая отражает оптимальность текущей конфигурации  манипулятора с точки зрения целевой задачи.

Эффективность используемых алгоритмов существенно зависит от вида целевой функции, поэтому определим вид целевой функцию . Поскольку алгоритм Левенберга-Марквардта является градиентным алгоритмом, целевая функция должна быть непрерывной и дифференцируемой. Принимая это во внимание, запишем целевую функцию в следующем виде:

где  – ошибка по положению схвата,  – ошибка по ориентации схвата,  – член, характеризующий положение схвата с точки зрения отсутствия коллизий, , ,  – соответствующие весовые коэффициенты.

Уравнение ошибки по положению   выглядит следующим образом:

где  – желаемое положение схвата манипулятора.

Уравнение ошибки по ориентации можно записать аналогичным образом, использую ошибку по углам Эйлера, однако более оптимальным вариантом является использование кватернионов, поскольку кватернионное представление позволяет избежать сингулярностей и разрывов, характерных для углов Эйлера, а также определяется меньшим числом параметров [20]:

где  – желаемый кватернион ориентации,  – текущий кватернион ориентации.

На локальном этапе будет использовать вид целевой функции, приведенный в (1), однако в рамках глобального этапа с применением PSO для удобства преобразуем данную целевую функцию таким образом, чтобы оптимизационный процесс выполнял задачу максимизации ее значения:

В рассматриваемом случае пространство поиска возможных решений ОЗК будет являться 2-мерным пространством, где каждому вектору  соответствует некоторое значение целевой функции 

Очевидно, в случае МИСП, имеющего 7 степеней подвижности, пространство поиска будет являться 7-мерным пространством, а искомый вектор – вектором , содержащим 7 значений обобщенных координат. В остальном применение метода роя частиц для ОЗК МИСП не отличается от ранее рассмотренного случая 2-звенного манипулятора.

Применение комбинированного подхода для решения ОЗК МИСП

Суть комбинированного подхода заключается в том, чтобы использовать сильные стороны каждого из алгоритмов в рамках рассматриваемой задачи. В таблице 1 приведены их оценочные характеристики.

Таблица 1.

Оценочные характеристики методов

Как видно из таблицы, достоинством PSO является высокая скорость сходимости целевой функции на начальном этапе поиска решения, а также способность решать многокритериальные задачи, что является необходимым для обеспечения коллизионной устойчивости. Однако по мере движения в области глобального оптимума скорость сходимости снижается. С другой стороны, алгоритм LM может «застревать» в локальных оптимумах, из-за чего не гарантирует нахождение решения, однако при попадании в окрестности глобального оптимума имеет высокую скорость сходимости целевой функции.

Таким образом, первый этап предложенного алгоритмического решения включает в себя применение PSO для нахождения окрестности глобального оптимума. Затем происходит смена алгоритмов – LM уточняет полученное на предыдущем этапе решение, перемещаясь в окрестности глобального оптимума до достижения конечного результата. Проиллюстрируем описанный подход следующей схемой (Рисунок 6):

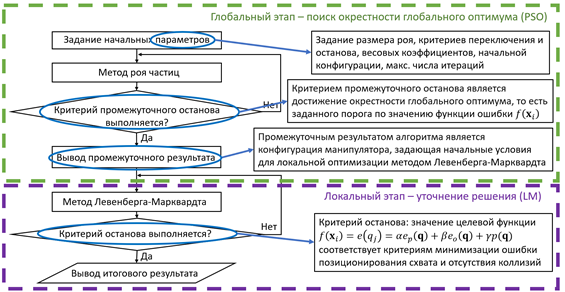
Рисунок 6. Схема комбинированного алгоритмического решения

Моделирование решения ОЗК для тестовых примеров

Как было упомянуто ранее, разработка оптимального алгоритмического решения ОЗК особенно актуальна для тех задач, которые робот-манипулятор выполняет в режиме реального времени. В связи с этим критически важным критерием оценки эффективности алгоритма является время решения им ОЗК. В данном случае решение ОЗК является итерационным процессом, поэтому это время соответствует длительности цикла сходимости целевой функции (1).

Длительность цикла сходимости целевой функции изначально представляет собой количество итераций, которое должен выполнить алгоритм для того, чтобы найти значение аргумента, соответствующего оптимальному значению целевой функции. В рамках практического применения значение имеет временная оценка длительности. Соответствие числа итераций и времени выполнения всего расчета определяется аппаратным обеспечением – в частности, процессором, выполняющим вычисления. В табл. 2 представлен период выполнения одной итерации для целевого процессора блока управления МИСП и высокопроизводительного тестового процессора.

Таблица 2.

Длительность итерационного цикла ОЗК

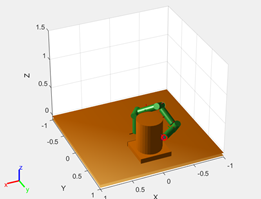
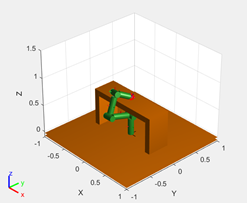
В задача реального времени цикл решения ОЗК манипулятора не должен превышать 100 мс [23]. Следовательно, за это время вычислительная мощность процессора блока управления МИСП позволит выполнить  итераций. Это значение было использовано для последующей оценки результатов моделирования для двух тестовых примеров с различными конфигурациями МИСП и целевых точек (рис. 7, а, в).

а                                                                           б

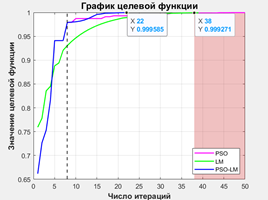
в                                                                               г

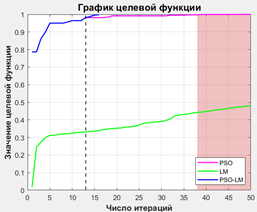
Рисунок 7. Результаты моделирования алгоритма: а, в – рабочие области манипулятора, б, г – графики сходимости целевой функции

Для каждого из примеров в ходе моделирования было проведено 5 экспериментов. В табл. 3 представлены значения целевой функции по истечении 38 итераций для каждого из модельных экспериментов в обоих примерах. Поскольку рассматриваемый подход включает в себя стохастический метод роя частиц, на основе результатов моделирования можно определить математическое ожидание  и дисперсию .

Таблица 3.

Результаты экспериментов

Отсюда среднее значение математического ожидания и дисперсии составляет  и  соответственно. Из формулы (3) можно вывести, что данное среднее значение математического ожидания соответствует ошибке положения схвата, равной , а также ошибке ориентации схвата, равной .

Таким образом, полученные результаты подтверждают эффективность предложенного подхода для решения ОЗК МИСП.

Заключение

В данной статье комбинирование метода роя частиц и алгоритма Левенберга-Марквардта было применено для решения ОЗК МИСП, функционирующего в реальном времени в условиях недетерминированной рабочей среды, что позволило получить эффективное алгоритмическое решение, применимое для управления реальным МИСП. По результатам моделирования полученного решения было выявлено, что в условиях реального времени данный подход позволяет решать ОЗК МИСП с точностью, соответствующей величине ошибки 1.5 мм по положению и 0.087° по ориентации схвата.