ПРОБЛЕМА НАХОЖДЕНИЯ МИНИМАЛЬНОГО РАЗРЕЗА: СРАВНИТЕЛЬНЫЙ АНАЛИЗ АЛГОРИТМОВ КАРГЕРА–ШТЕЙНА И ШТЁРА–ВАГНЕРА

Аннотация. В статье представлено сравнение эффективности двух алгоритмов нахождения минимального разреза: Каргера–Штейна (вероятностного) и Штёра–Вагнера (детерминированного).

Ключевые слова: минимальный разрез, Штер–Вагнер, Каргер–Штейн.

Пусть задан граф  , где  — множество вершин,  — множество рёбер, а  — функция весов. Минимальный разрез определяется как разбиение множества вершин  на два непересекающихся подмножества  , такое что суммарный вес рёбер, функция стоимости (cost function) минимальна:

                                                                                     (1)

где, .

Алгоритм Каргера–Штейна основан на случайных сжатиях рёбер. На каждом шаге выбирается ребро (с вероятностью, пропорциональной его весу), вершины объединяются, и процесс продолжается, пока не останется две вершины. Разрез между ними и есть решение. Повторяя алгоритм  раз, можно гарантировать вероятность ошибки менее  . Временная сложность: , где . Алгоритм Штёра–Вагнера основан на последо-вательном объединении вершин с учётом весов рёбер. Для каждой пары вершин вычисляется разрез, а затем одна из них «поглощается» другой. Временная сложность: , где , . Минимальный разрез определяется как наименьший из полученных.

Ниже представлены результаты запуска алгоритма Каргера-Штейна и Штер-Вагнера на наборе файлов, с заданным числом вершин (vert), ребер (edg).

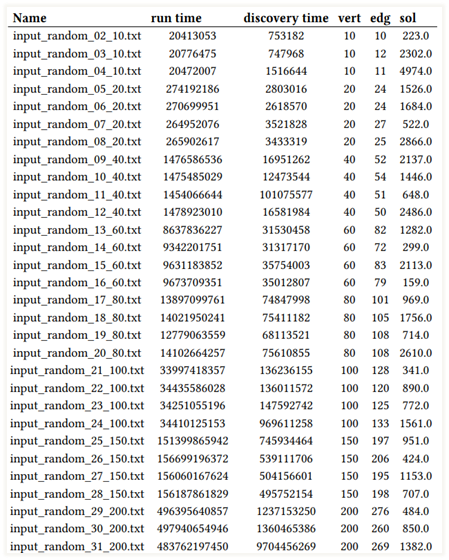
Рисунок 1. Результаты алгоритма Каргера-Штейна

Таблица демонстрирует результаты измерений, где run time это полное время работы алгоритма от старта до завершения. Оно отражает общую вычислительную сложность; discovery time — это момент в процессе работы, когда алгоритм впервые находит правильный ответ. Эта метрика показывает, как быстро алгоритм приходит к верному решению, даже если после этого он продолжает работать для его подтверждения. Атрибут sol (solution) — это ответ на задачу, стоимость минимального разреза. На рисунке ниже, представлены результаты работы алгоритма Штера-Вагнера:

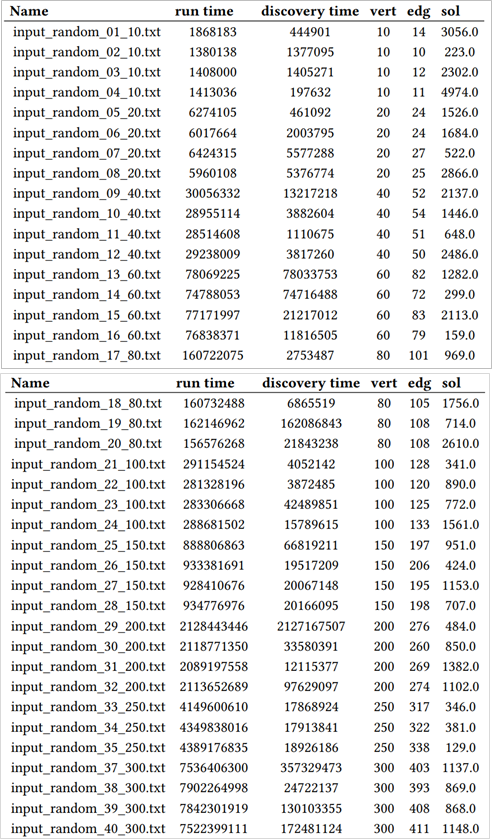
Рисунок 2. Результаты алгоритма Штера-Вагнера

Для понимания данных, на рисунке ниже, представлен график изменения run time в зависимости от числа ребер (edges) и вершин (vertices):

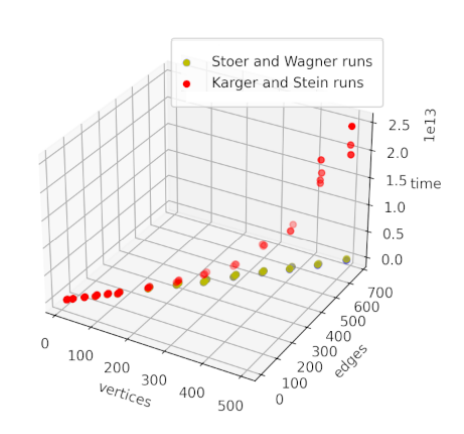
Рисунок 3. Cравнение run time двух алгоритмов

Экспериментальный анализ времени выполнения алгоритмов полностью соответствует теоретическим ожиданиям, выведенным из анализа их сложности. Результаты подтверждают, что алгоритм Каргера-Штейна демонстрирует худшую производительность по сравнению с алгоритмом Штера-Вагнера.