Реализация адаптивного алгоритма самоорганизации нечеткой сети

Аннотация. В рамках исследования рассмотрены существующие алгоритмы самоорганизации нейронный сетей. Установлено, что наиболее универсальным с точки зрения знания количества центров представляется адаптивных алгоритм, автоматически добавляющий новые центры в режиме online в зависимости от распределения входных данных. Целью исследования является реализация адаптивного алгоритма самоорганизации нечеткой сети. В ходе экспериментальных исследований проведен анализ полученных результатов и сделан вывод о применимости алгоритма при различных входных данных.

В настоящее время актуальной задачей современной информатики является разработка и реализация алгоритмов нечетких сетей, основанной на активном использовании методического, технологического, алгоритмического и программного заделов из предшествующих проектов.

Несмотря на значительное количество уже известных практических приложений искусственных нейронных сетей, возможности их дальнейшего использования для обработки сигналов не изучены окончательно, и можно, высказать предположение, что нейронные сети еще в течение многих лет будут средством развития информационной техники.

Однако особое внимание следует уделить нечетким нейронным сетям, характерной особенностью которых является возможность использования нечетких правил вывода для расчета выходного сигнала, что отражается в многочисленных научных работах на данную тематику.

Так, например, в работе [1] авторами описывается метод, который включает в себя нечеткое моделирование Такаги – Сугено (TS) с двумя подходами кластеризации данных, включая кластеризацию нечетких c-средних (FCM) и субтрактивную кластеризацию для оценки модуля деформации массива горных пород. Информация, возвращаемая нечеткой кластеризацией, первоначально использовалась для определения количества правил и предшествующих функций принадлежности, а затем линейной оценки наименьших квадратов, реализованной для получения нечетких последовательных параметров. Адаптивная система нейро-нечеткого логического вывода (ANFIS) была применена, чтобы модифицировать заранее определенные структурные модели на основе кластеризации TS для улучшения характеристик их обобщения.

Авторами в статье [2] была предложена модель сверточной нечеткой нейронной сети для классификации изображений. В данной статье описывается обучение сверточной нечеткой нейронной сети состоящее из трех независимых этапов для трех компонентов сети.

В статье [3] предлагается новый метод оценки параметров нечеткой модели Такаги-Сугено при наличии неполных данных. Также описывается механизм вывода, который может работать с неполными данными. Представленный метод имеет дополнительное преимущество, заключающееся в том, что он не требует итеративной оценки вероятности пропущенных значений.

В работе [4] представлены результаты исследования, проведенного для изучения влияния выбора алгоритма кластеризации на общую производительность нечеткой гидрологической модели. Исследование иллюстрируется на примере разработки нечеткой модели Такаги – Сугено для прогнозирования притока в водохранилище в бассейне Нармада, Индия. Модель была разработана с использованием двух популярных методов кластеризации, а именно, Густафсона-Кесселя (GK) и вычитающей кластеризации (SC), и была тщательно оценена на эффективность на основе различных статистических показателей.

В книге [5] приведен адаптивный алгоритм самоорганизации нечеткой сети, сформулированный для обобщенной модели Ванга-Менделя. Данный алгоритм был сформирован только для гауссовской функции в статье [6]. В результате реализации данного алгоритма определяются: количество центров и их расположений в части, соответствующим условиям и заключениям.

В ходе данного исследования был разработан алгоритм, представленный в книге [5].  

На рисунках 1, 2, 3 представлены результаты аппроксимации кривой

f(x)=2,1sin(1,2πx)+2,3sin(3,2πx)+2,5sin(5,2πx)

нечеткой сетью с самоорганизацией при использовании адаптивного алгоритма обучения.

Непрерывная линия обозначает ожидаемые значения, а пунктирная линия фактические значения.

На рисунке 1 представлены результаты, полученные при величине порога r=0,5.

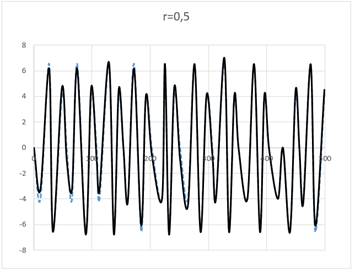
Рисунок 1. Реализация алгоритма при r=0,5

На рисунке 2 представлены результаты, полученные при величине порога r=0,2.

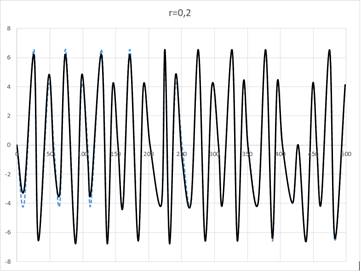
Рисунок 2. Реализация алгоритма при r=0,2

На рисунке 3 представлены результаты, полученные при величине порога r=0,05.

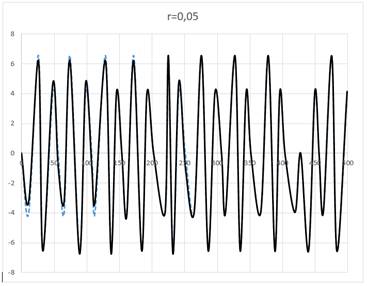
Рисунок 3. Реализация алгоритма при r=0,05

В таблице, расположенной ниже, представлена зависимость количества кластеров М от заданной величины r – предельного евклидового расстояния между x и центром.

Таблица.

Зависимость количества кластеров M от величины r

График зависимости М от r представлен на рисунке 4.

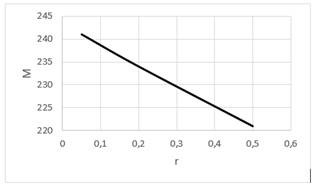
Рисунок 4. График зависимости М от r

Было замечено, что при малом значении r количество кластеров возрастает, в результате чего аппроксимация данных становится более точной, однако это достигается за счет более сложной функции и увеличения объема необходимых вычислений при одновременном ухудшении обобщающих свойств сети.