Предварительно напряженный амортизатор сжатия в упругой подвеске агрегата

Prestressed Compression Shock Absorber in the elastic suspension of the unit

Kirill Golyakov

Magistrates Kuban State Technological University, Russia, Krasnodar

Vitaly Kovalevsky

Doctor of technology, Kuban State Technological University, Russia, Krasnodar

Аннотация. В статье рассмотрен амортизатор, воспринимающий знакопеременные нагрузки вибрационного типа в однокаскадной упругой подвеске агрегата. Конструкция амортизатора обеспечивает безударные колебания агрегата при соответствующей затяжке менее податливого нижнего упругого элемента. Определены условия, при которых исключается появление зазора в амортизаторах подвески агрегата. Получены рациональное соотношение жесткостей упругих элементов в опоре и минимально необходимая сила затяжки.

Abstract. The article describes a shock absorber that perceives alternating loads of vibration type in a single-stage elastic suspension of the aggregate. The design of the shock absorber provides unstressed oscillations of the aggregate in the presence of a protracted, less pliable lower elastic element. Certain conditions under which the appearance of a gap in the shock absorbers of the aggregate suspension is excluded. Rational correlations of rigid and elastic elements in the support and the minimum necessary tension force are obtained.

Ключевые слова: виброизоляция; агрегат; амортизатор; упругий элемент; деформация; сила затяжки; жесткость; динамическая сила.

Keywords: vibroinsulation; aggregate; absorber; resilient element; deformation; strap force;  hardness; dynamic force.

Устройство амортизатора, показанного на рис.1, имеет два упругих элемента: верхний представляет собой резиновый цилиндр с осевым отверстием ступенчатой формы, нижний выполнен в виде резиновой цилиндрической шайбы. Конструкция представляет собой предварительно напряженный резиновый (полимерный) амортизатор сжатия для восприятия знакопеременных нагрузок вибрационного типа.

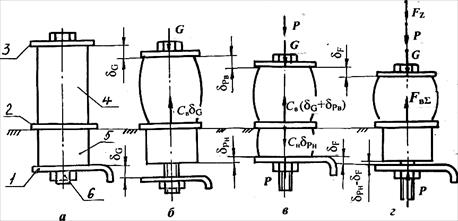
Рисунок. 1. Упругие деформации элементов амортизатора под действием сил собственного веса агрегата G, предварительной затяжки P и динамической нагрузки F_z: 1 – лапа агрегата; 2 – рама (фундамент); 3 – шайба; 4, 5 – верхний и нижний упругие элементы; 6 − болт

Все амортизаторы в подвеске агрегата работают параллельно, т.е. упругая подвеска однокаскадная. Требуется уменьшить возмущающее воздействие агрегата на раму (фундамент, перекрытие). Эффективной виброизоляция будет, если сила воздействия на раму F_ф по модулю существенно меньше возмущающей силы F_z, т.е. ǀF_фǀ<<ǀF_zǀ. Это условие обеспечивается в амортизирующей подвеске, имеющей обоснованную податливость, в связи с чем, требуется аналитическая оценка жесткостных характеристик подвески. Во избежание больших амплитуд деформаций амортизаторов, возникающих вследствие резонансов при пусках и остановах агрегатов, следует иметь нелинейную характеристику жесткости упругих элементов амортизатора.

Податливость стержня болта и металлических элементов опоры несоизмеримо малы по сравнению с податливостью резиновых (полиуретановых) элементов, поэтому можно принять, что упругие перемещения лап агрегата происходят только благодаря податливости последних. Схема действующих в амортизаторе сил и деформаций представлена на рис.1.

Под действием силы собственного веса опора из состояния а переходит в состояние б в результате деформации δ_G верхнего элемента. На величину деформации δ_G лапы агрегата перемещаются вниз. Завинчиванием гайки выбирается зазор между лапой и нижним упругим элементом и выполняется затяжка болта, от которой верхний и нижний элементы получают деформации сжатия δ_Pв и δ_Pн соответственно. Такое состояние виброопоры является исходным рабочим положением (рис.1,в).

Условия пуска и останова агрегата, например, мотор-компрессора, таковы, что могут возникать собственные колебания системы с частотой ω_с. После пуска или останова запас энергии собственных колебании расходуется на преодоление сопротивлений в опорах (внешнее и внутреннее трение), в результате собственные колебания системы затухают. Затем агрегат совершает вынужденные колебания под действием возбуждающей гармонической силы Fsinωt с частотой ее проявления ω.

Максимальное перемещение лапы агрегата 1 при вынужденных колебаниях равно их амплитуде, которая определяется нелинейной зависимостью [1]

x₀ = F_z/C_в^"(1−ω²/ω²_с) = x_ст/(1−ω²/ω²_с) = x_стk = δ_F,                                                                            (1)

где x_ст = F_z/C_в^" – деформация сжатия верхнего упругого элемента с жесткостью C_в^", если к нему приложить статистически постоянную нагрузку F_z равную амплитуде возбуждающей силы Fsinωt; ω_с − собственная частота системы;

k = 1−ω²/ω²_с – коэффициент усиления (динамичности).

Зависимость (1) запишем в виде

δ_F = kF_z/C_в^" или kF_z = δ_FC_в^" = ma,                                                                                           (2)

где a − амплитуда ускорения колебания массы агрегата; m − масс агрегата, приходящаяся на одну опору.

Динамическая сила kF_z колеблющейся массы агрегата является силой возмущающего воздействия, которая передается на раму через упругие элементы опоры. При направлении этой силы вниз лапа агрегата перемещается вниз на величину упругой деформации сжатия верхнего элемента δ_F, предварительная деформация сжатия нижнего элемента δ_Pн уменьшается до Δ = δ_Pн−δ_F._. Если

δ_F˃ δ_Pн, то между лапой и нижним элементом появится зазор, что недопустимо из-за возможных ударов в амортизаторе.

Определим условия, при которых зазор в амортизаторе не возникает. Для этого рассмотрим равенство внешних и внутренних сил в амортизаторе находящемся последовательно в состояниях в и г (рис.1). Сила затяжки в верхнем элементе P = C_в^ʹδ_Pв, в нижнем элементе P = C_н^ʹδ_Pн отсюда

C_в^ʹδ_Pв= C_н^ʹδ_Pн.                                                                                                               (3)

Здесь C_в^ʹ, C_н^ʹ − жесткости верхнего и нижнего элементов при деформациях соответственно δ_Pв и δ_Pн (с учетом нелинейной жесткости).

Запишем условие равновесия сил в опоре, находящейся в состоянии, показанном на рис.1,г,

C_вδ_G+C_в^ʹδ_Pв+C_в^"δ_F−C_н(δ_Pн−δ_F)+Р = G+ kF_z+ Р                                

Так как G = C_вδ_G, то с учетом равенства (3) имеем:

C_в^"δ_F+ C_н^ʹδ_F = kF_z,  δ_F = kF_z/(C_в^"+ C_н^ʹ),                                                                                          (4)

где C_в^" − жесткость верхнего элемента при его деформации равной δ_G+δ_Pв+δ_F.

Отсутствие зазора в опоре выражается условием δ_Pн−δ_F ≥ 0, а, так как.

δ_Pн = P/C_н^ʹ, то запишем

P/C_н^ʹ = kF_z/(C_в^"+ C_н^ʹ) или P/kF_z = C_н^ʹ/(C_в^"+C_н^ʹ) = 1/(C_в^"/C_н^ʹ)+1.                                                                    (5)

Из полученной зависимости (5), представленной на рис.2 видим, что требуемая сила затяжки тем меньше, чем меньше жесткость нижнего элемента.

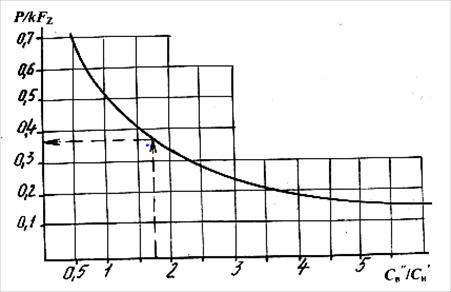
Рисунок. 2. Влияние жесткостей упругих элементов амортизатора на затяжку болта

Если стремиться к возможно меньшей суммарной силе сжатия Р_Σ верхнего упругого элемента, то рациональное отношение C_в^"/C_н^ʹ найдется из зависимости Р_Σ/G = f(C_в^"+C_н^ʹ), которую получим, воспользовавшись зависимостями (5).

Суммарная сила сжатия равна

Р_Σ = G+P+kF_z = G+kF_z/((C_в^"/C_н^ʹ)+1)+kF_z..                                                                                  (6)

Так как G = mg, kF_z = ma_z, то kF_z/G = a_z/g, где g = 9,81 м/с², m – масса агрегата, которая приходится на одну опору, a_z − вертикальная составляющая ускорения колебательного движения.

Выполнив подстановки и разделив обе части равенства на G, получим

Р_Σ/G = 1+(a_z/g)[1/((C_в^"/C_н^ʹ)+1)+1],

Р_Σ/G = (1/(C_в^"/C_н^ʹ)+1)[(C_в^"/C_н^ʹ)((a_z/g)+1)+2(a_z/g)+1].                                                                            (7)

На рис.3 зависимость (7) представлена графически в виде номограммы для различных значений a_z/g. Из графиков номограммы видно, что значение суммарной силы зависит от ускорения колебательного движения a_z и увеличивается с увеличением жесткости нижнего упругого элемента C_н^ʹ. С увеличением

отношения C_в^"/C_н^ʹ эффективность снижения силы Р_Σ уменьшается.

Если условиться считать, что с каждым последующим увеличением C_в^"/C_н^ʹ на единицу снижение силы Р_Σ менее, чем на 5% неэффективно, то рациональные значения C_в^"/C_н^ʹ найдутся пересечением кривых рассматриваемых зависимостей с кривой а, соответственно для 10% − пересечением с кривой б.

Рисунок 3. Номограмма для определения влияния соотношения жесткостей упругих элементов амортизатора на суммарную силу сжатия в опоре

По найденному рациональному значению соотношения C_в^"/C_н^ʹ и известному значению силы kF_z по рис.2 определяется минимально необходимая сила затяжки болта P.