Исследование самотормозящихся кулачковых соединений
Журнал: Научный журнал «Студенческий форум» выпуск №2(95)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №2(95)
Исследование самотормозящихся кулачковых соединений
THE STUDY OF THE SELF-LOCKING CAM CONNECTIONS
Sergey Chepaykin
Student, Togliatti State University, Russia, Togliatti
Kozlov Anton
Candidate of Technical Sciences, Associate Professor, Department, Togliatti State University, Russia, Togliatti
Аннотация. В данной статье представлен расчёт клинового самотормозящегося соединения в программе Ansys v14. Определены возникающие силы, а также отображены графики зависимости силы трения и момента трения относительно момента затяжки.
Abstract. This article presents the calculation of a wedge self-braking connection in the Ansys v14 program. The arising forces are determined, and also graphs of the dependence of the friction force and the friction moment relative to the tightening moment are displayed.
Ключевые слова: болтовое соединение, метизы, клиновая пробка.
Keywords: bolted connection, hardware, wedge plug.
Обычно в отверстие соединяемых деталей болт вставляется с зазором и соединение осуществляется затяжкой гайки, что создаёт давление между деталями, препятствующее их расхождению под действием осевых сил и относительно сдвигу под действием поперечных сил, благодарю возникающему между деталями трению. Реже болт плотно входит в отверстие соединяемых деталей и препятствует относительному их сдвигу под действием поперечных сил, работая на срез, в этом случае стержень болта и отверстие болта обрабатываются с высокой точностью и при этой же поперечной силе болт получается тоньше [2, c. 13].
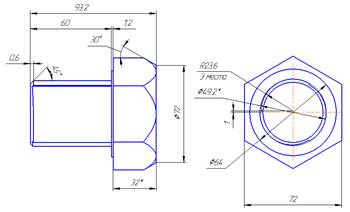
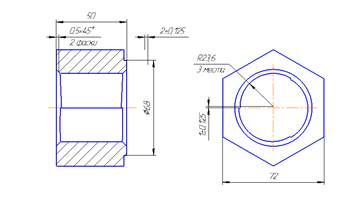
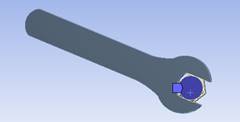
Рисунок 1. Клиновый болт и клиновая гайка
В нашем случае представлен клиновый болт и клиновая гайка (Рисунок 1), сопрягаемые поверхности которых представляют собой кулачково-клиновую спираль, которая позволяет выполнить соединение с нужным моментом, затрачивания на это минимум времени. Прикладываемые силы при выполнении такого соединения сопоставимы с силами на болтовом резьбовом соединении.
Нам необходимо провести 3 эксперимента с разным прикладываемым моментом: 50 Н∙м; 250 Н∙м и 340 Н∙м и определить процессы, возникающие при расчёте. Расчёт производился в программе ANSYS V14, в модуле Structural Analysis.
Рассмотрим пример расчета для образца с нагрузкой 50 Н∙м. В качестве материала детали выбираем по умолчанию конструкционную сталь [1, с. 9].
Загружаем нашу геометрию (Рисунок 3) и задаем размер сетки конечных элементов (Рисунок 4) [1, с. 10].
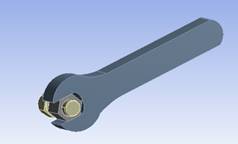

Рисунок 4. Сетка конечных элементов
Фиксируем на нашей геометрии плоскости, которые не должны перемещаться при прикладывании нагрузки (Рисунок 5).

Рисунок 5. Фиксация плоскости
Задаем вектор силы и прикладываем нагрузку 50 Н×м, которая действует на рожковый ключ [1, с 13]. Направление вектора указано согласно направлению закручивания гайки на болте.
Выбираем в качестве заделки торцевую поверхность головки болта [3, c. 98], т.к. именно этот элемент являются неподвижными в процессе закручивания гайки.
|
|
|
|
Рисунок 6. Вектор силы и нагрузка на ключ |
Рисунок 7. Выбор заделки |
Повторяем все действия для оставшихся 2-ух экспериментов, изменяя при это лишь прикладываемую нагрузку.
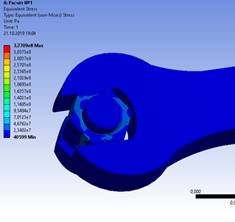
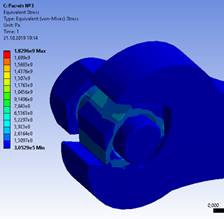
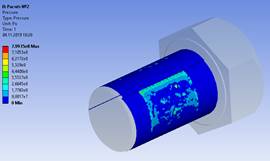
В результате проведения 3-х экспериментов получаем величину эквивалентного напряжения (Рисунок 8) и контактного давления, которое будет испытывать наше соединение (Рисунок 9) [1, с. 17].
|
|
|
|
|
|
|
Рисунок 8. Эквивалетное напряжение |
|
|
|
|
|
|
|
|
Рисунок 9. Контакное давление |
|
На основании полученных результатах определяем усредненную величину контактного давления на рабочих поверхностях для 3-ёх экспериментов, которая будет равна:
- для первого эксперимента 100053602, 28 Па;
- для второго эксперимента 44535333 Па;
- для третьего эксперимента 60899875,85 Па
Рассчитываем силу нормального давления на контактных площадках для каждого из экспериментов:
![]() (1)
(1)
![]()
![]()
![]()
где ![]() – давление в Па;
– давление в Па; ![]() = площадь 3-ех контактных площадок в м2.
= площадь 3-ех контактных площадок в м2.
Определяем силу трению, которая препятствует разделению соединения:
![]() (2)
(2)
![]()
![]()
![]()
где ![]() – коэффициент трения;
– коэффициент трения;
![]() – сила нормального давления.
– сила нормального давления.
Высчитываем момент трения в нашем соединении:
![]() (3)
(3)
![]()
![]()
![]()
где ![]() – сила трения;
– сила трения; ![]() – радиус поверхности контакта.
– радиус поверхности контакта.
На основании полученных данных строим графики зависимости.
|
|
|
|
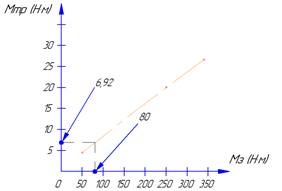
Рисунок 10. Зависимость момента трения от момента затяжки |
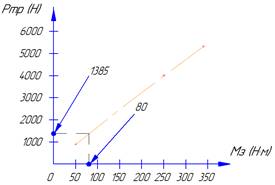
Рисунок 11. Зависимость силы трения от момента затяжки |
Полученные значения свидетельствует о том, что данное соединение способно выполнять своё служебное назначение при моменте затяжки 80 Н∙м, при этом коэффициенте запаса составляет 11%.