Обучение схематизации и моделированию в процессе решения текстовых задач в начальной школе как основа формирования метапредметности

Федеральный государственный образовательный стандарт начального общего образования последнего поколения выдвигает требования к овладению обучаемыми не только предметными, но и метапредметными умениями, основу которых составляют коммуникативные, познавательные, регулятивные и личностные универсальные учебные действия (УУД) [6, с. 7]. Математика как учебный предмет представляет собой полигон для формирования познавательных УУД, к числу которых, прежде всего, относят: действия схематизация, моделирования и конструирования, логические УУД, постановка и решение проблемы, работа с информацией, представленной в различных формах (вербальной, иллюстративной, схематической, табличной и условно-знаковой) [1].

Особую роль в формировании обозначенных нами умений занимает обучение младших школьников решению математических задач. Под математической задачей понимают  проблемную ситуацию, которую решают путем использования математических методов и приемов. Среди математических задач выделяют текстовые задачи, представляющие собой описание на естественном языке некоторого явления, ситуации или процесса. В текстовой задаче обычно описывается не все явление в целом, а лишь некоторые его стороны и, главным образом, его количественные характеристики. С точки зрения моделирования, текстовая задача уже есть словесная модель некоторой реальной ситуации [2].

Моделирование в решении текстовых задач начинается с построения высказывательной модели: здесь учащиеся выявляют, о каких объектах идет речь в задаче, устанавливают исходные (известные) и подлежащие определению величины, определяют условия (утверждения) и требования, то есть вопрос, на который необходимо найти ответ.

На начальном этапе обучения решению текстовых задач, в связи с тем, что у детей младшего школьного возраста преобладает наглядно-образное мышление, учитель в качестве наглядности использует вспомогательные схемы и модели, которые можно разделить на схематизированные и знаковые по видам средств, используемых для построения [4]. Схематизированные модели, в свою очередь, делятся на вещественные и графические, в зависимости от того, какое действие они обеспечивают. Вещественные модели текстовых задач обеспечивают физическое действие с предметами. Графические модели используются, как правило, для обобщенного, схематического воссоздания ситуации задачи. К графическим следует отнести следующие виды моделей: рисунок, условный рисунок, чертеж, схематичный чертеж, блок-схему [5, с. 185].

Рассмотрим на конкретном примере для 1 класса, каким образом реализуются описанные нами модели при решении младшими школьниками текстовых задач.

Задача. Диана прочла за летние каникулы 5 книг, а Света на 3 книги меньше. Сколько всего книг прочли девочки?

Для данного примера высказывательная модель принимает следующий вид:

- объекты: книги;

- утверждения: 1) Диана прочла 5 книг. 2) Света прочла на 3 книги меньше;

- требования: 1) Сколько книг прочла Света? 2) Сколько всего книг прочли девочки?

Составим вспомогательные модели для данной задачи:

1. Рисунок.

Рисунок изображает реальные предметы, о которых говорится в задаче (рис. 1).

Рисунок 1. Графическая модель: рисунок

Знак фигурной скобки означает, что необходимо найти общее количество книг, прочитанных девочками, то есть сложить количество книг, прочитанное Дианой и количество книг, прочитанное Светой. Таким образом, на рисунке мы также можем использовать знаки и символы.

2. Условный рисунок: предметы заменены геометрическими фигурами.

Рисунок 2.Графическая модель: условный рисунок

3. Чертеж, представляющий собой условное изображение предметов, взаимосвязей между ними и взаимоотношения величин с помощью отрезков и с соблюдением определенного масштаба. На рис. 3 один отрезок означает 1 книгу. 

Рисунок 3. Графическая модель: чертеж

4. Схематичный чертеж (или просто схема) – это чертеж, на котором все взаимосвязи и взаимоотношения величин передаются приблизительно без соблюдения масштаба (рис. 4).

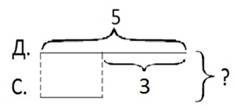
Рисунок 4. Графическая модель: схема

5. Блок-схема.

При изучении текстовых задач блок-схемы используются в процессе составлении плана решения задачи, как, например, на рис. 5. Выполняя последовательно действия снизу вверх (нижняя ступень – первое действие, верхняя ступень – второе действие), ученики находят, сколько всего книг прочли девочки.

Рисунок 5. Графическая модель: блок-схема

Рисунки, схемы, чертежи и блок-схемы не только помогают учащимся в осознанном выяснении скрытых зависимостей между величинами, но и побуждают детей активно мыслить, искать наиболее рациональные пути решения задачи, применять знания и умения на практике. Схематизация дает возможность более полно увидеть отражение зависимостей между данными и искомыми в задаче, увидеть задачу в целом, помогает обобщить теоретические знания.

Знаковые модели могут быть выполнены как на естественном, так и на математическом языке. К знаковым моделям, выполненным на естественном языке, относят краткую запись задачи и таблицы.

Таблица как вид знаковой модели используется главным образом тогда, когда в задаче имеется несколько взаимосвязанных величин, каждая из которых задана одним или несколькими значениями. Табличный метод широко используется при решении задач на различные процессы [3].

Краткая запись есть представление в лаконичной форме содержания задачи, выполненное с помощью опорных слов, простых математических выражений. В краткой записи представлены значения исходных величин и связи между данными и искомыми величинами (рис. 6). Краткая запись должна наглядно представлять высказывательную модель: отражать объекты, условия и требования.

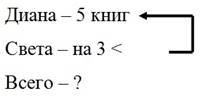
Рисунок 6. Графическая модель: краткая запись

К знаковым моделям относятся и так называемые памятки-сигналы (табл. 1), которые должны помочь учащимся в выборе правильного действия.

Таблица 1.

Памятки-сигналы

Математическая модель представляет собой вид знаковой модели. В начальной школе в процессе решения текстовых задач используются следующие математические модели:

- решение задачи по действиям с пояснениями, без пояснений или с вопросами (арифметический способ решения задачи);

- решение задачи в виде выражения (арифметический способ решения задачи);

- решение задачи с помощью составления уравнения (алгебраический способ решения задачи).

Для нашей задачи математические модели принимают вид:

1) 5 – 3 = 2 (кн.) – прочла Света.

2) 5 + 2 = 7 (кн.) – прочли обе девочки;

или

(5 – 3) + 5 = 7 (кн.) – прочли обе девочки.

Ответ: 7 книг.

В заключение отметим, что схематизация и моделирование являются весьма эффективным и наглядным средством обучения школьников решению текстовых задач и способствует включению в учебный процесс всех учащихся класса. Схемы и модели, способствующие организации деятельности, дают возможность школьникам овладеть следующими видами УУД:

- регулятивные: самостоятельная постановка  цели, планирование деятельности, осуществление самоконтроля и рефлексии, коррекция действий на каждом этапе построения модели;

- коммуникативные: формулировка целей и задач, планирование деятельности и проговаривание плана во внешней речи, постановка вопросов к задаче и формулирование ответов на них;

- личностные:  осмысленное исследование реальных жизненных ситуаций, формирование целеустремленности и настойчивости в достижении целей;

- познавательные: составление и преобразование моделей, логические действия (анализ, классификация, обобщение и др.), информационные действия: поиск недостающей информации, восполнение информационных пробелов, определение существенной и несущественной для решения задачи информации.

Таким образом, решению текстовых задач в начальной школе следует уделять повышенное внимание, так как использование различных приемов моделирования и составления схем позволяет сформировать у младших школьников целый спектр УУД, что положительно сказывается на освоении учащимися программного материала.