Моделирование в процессе решения сюжетных задач в начальном курсе математики

Вспомним, что моделирование – это важнейшая логическая (мыслительная) операция, благодаря которой человек способен решать жизненные ситуации и находить верное решение проблем. Актуальность проблемы обучения моделированию в начальной школе трудно переоценить, так как моделирование, как познавательное универсальное учебное действие, школьники необходимо должны осваивать согласно требованиям федерального государственного образовательного стандарта  начального общего образования последнего поколения [5, с. 7].

Особую роль в обучении приемам моделирования отводят текстовым и сюжетным задачам. Напомним, что под текстовой задачей понимают описание некоторой жизненной ситуации (сюжета), явления или процесса, на естественном или математическом языке с определенными требованиями, либо установить наличие или отсутствие отношений между объектами, либо определить вид этого отношения, либо дать количественную характеристику какого-то компонента задачи [4, с. 157].

Процесс решения любой задачи, в том числе и текстовой, можно анализировать с разных позиций. Так весь процесс можно рассматривать как процесс последовательного перехода от одной модели задачи к другой, например, как переход от словесной модели в виде текста к образной модели, а от нее к схематизированной, а затем символической, построенной с помощью математической символики [2].

Моделирование - построение и изучение моделей реально существующих объектов, процессов или явлений с целью исследования объектов познания на их моделях. Таким образом, основным понятием является понятие модели – упрощенного представления о реальном объекте, процессе или явлении. Под моделью также понимается объект, который отражает некоторые стороны изучаемого объекта или явления, существенных с точки зрения моделирования [1].

Перевод текста с естественного языка на математический – сложный процесс. Чтобы облегчить его – строят вспомогательные модели, тогда процесс решения задачи можно рассматривать как переход от одной модели к другой: от словесной модели к вспомогательной, от нее – к математической, на которой и происходит решение задачи.

Именно благодаря грамотному построению и исследованию модели текстовой задачи процесс ее решения становится доступным ребенку. Рассмотрим на конкретном примере для младших школьников, каким образом реализуются этапы моделирования при решении ими текстовых задач.

Задача 1. Витя и Катя одновременно вышли навстречу друг другу из своих домов, расстояние между которыми 18 км. Скорость мальчика 5 км/ч, а девочки – 4 км/ч. Через какое время они встретятся?

На первом этапе работы с задачей, школьники строят высказывательую модель, а именно, находят объекты задачи: дети (мальчик Витя и девочка Катя) и определяют:

· процесс: движение навстречу друг другу;

· известные величины: расстояние, скорости движения детей;

· искомые величины: время встречи;

· взаимосвязь между величинами: S = V × t, t = S : V, V = S : t.

На втором этапе работы с задачей, составляют план решения задачи. Поиск плана решения задачи является трудным процессом, который точно не определен. Можно только указать некоторые приемы, которые позволят осуществить этот этап. Одним из наиболее известных приемов поиска плана решения задачи арифметическим способом является разбор задачи по тексту или по ее вспомогательной модели. Разбор задачи по тексту проводится в виде цепочки рассуждений, которая может начинаться как от данных задачи, так и от ее вопросов. Проведем такой разбор по тексту задачи от вопроса к данным.

В задаче требуется узнать время встречи Вити и Кати. Значит, для выполнения требования задачи достаточно узнать, какое расстояние было между их домами и скорость, с которой дети сближались, то есть скорость сближения. Расстояние известно по условию, а скорость сближения нужно найти. Для этого надо сложить скорости мальчика и девочки. Затем, зная скорость сближения, можно найти и требование задачи, то есть время, через которое они встретятся. Для этого нужно разделить расстояние между домами на скорость сближения. Эти рассуждения можно представить в виде схемы (рис. 1).

Рисунок 1. Разбор задачи по тексту от вопроса к данным

На рис. 1 составлен план решения задачи, который является схематичной моделью ее решения.

На этапе работы с задачей огромную роль в понимании ее структурных компонентов и отношений между ними играют вспомогательные модели. В задачах на движение преимущественно используются графические модели, в частности, вспомогательный чертеж, и таблица (табличная модель).

К сформулированной нами задаче можно составить вспомогательный чертеж, представленный на рис. 2.

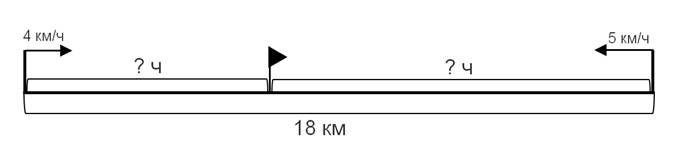
Рисунок 2. Вспомогательный чертеж

Табличная модель похожа на краткую запись. Этот способ нагляден и предназначен для решения определенного класса задач, в частности для решения задач на процессы (движение, работа, «купля-продажа»).

К данной задаче подходит следующая таблица.

Таблица 1.

Вспомогательная табличная модель

После построения вспомогательной модели к задаче необходимо проверить: все ли объекты задачи и их величины показаны на модели; все ли отношения между ними отражены; все ли числовые данные приведены; есть ли вопрос (требование) и правильно ли он указывает искомое.

Основными методами решения текстовых задач являются арифметический и алгебраический методы. Арифметический и алгебраический способы решения задачи представляют собой решающие математические модели [3, с. 207]. Решить задачу арифметическим методом – это значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Алгебраический способ решения задачи предполагает составление уравнения, неравенства или их систем.

Одну и ту же задачу можно решить различными арифметическими способами, они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи. Для текстовых задач, решаемых арифметическим способом, используются следующие приемы решения задач и ее оформления: по действиям без пояснений, по действиям с пояснениями, по действиям с вопросами, в виде выражения.

Решение задачи по действиям без пояснений:

1) 5 + 4 = 9 (км/ч);

2) 18 : 9 = 2 (ч).

Ответ: дети встретятся через 2 часа.

Решение задачи по действиям с пояснениями:

1) 5 + 4 = 9 (км/ч) – скорость сближения;

2) 18 : 9 = 2 (ч) – время, через которое они встретятся.

Ответ: 2 ч.

Решение задачи с вопросами:

1. Какова скорость сближения детей?

5 + 4 = 9 (км/ч).

2. Через какое время дети встретятся?

18 : 9 = 2 (ч).

Ответ: 2 ч.

Решение задачи выражением:

18 : (5 + 4) = 2 (ч).

Ответ: дети встретятся через 2 часа.

В процессе решения текстовой задачи особую актуальность имеет проверка полученного решения, что фактически представляет собой проверку адекватности составленной математической решающей модели. Проверка решения задачи может проходить с использованием следующих приемов:

1. решение задачи несколькими способами;
2. формулирование обратной задачи и ее решение.

Продемонстрируем указанные приемы применительно к нашей задаче.

1) Решение задачи еще одним способом (алгебраическим).

Пусть Витя и Катя встретились через x часов, значит, Катя прошла 4x км, а Витя – 5x км. Так как оба прошли 18 км, значит можно составить и решить уравнение:

4x + 5x = 18;

9x = 18;

x = 18 : 9;

x = 2 (ч) – время сближения.

Отметим, что в начальной школе, ученики решают уравнения с опорой на взаимосвязь компонентов действий.

2) Формулирование обратной задачи: Витя и Катя одновременно вышли навстречу друг другу из своих домов. Скорость мальчика 5 км/ч, а девочки – 4 км/ч. Через 2 часа они встретились. Какое расстояние было между детьми?

Текстовые задачи и их решение занимают в обучении школьников весьма существенное место и по времени, и по их влиянию на умственное развитие ребенка. Важно, чтобы учитель имел глубокие представления о текстовой задаче, о ее структуре, умел решать такие задачи различными способами и передавал эти знания своим ученикам.

Решение текстовых задач и нахождение разных способов их решения на уроках математики  способствует развитию у детей умений работать с информацией, представленной в различной форме: текстовой, табличной, символьной, а также развитию мышления, памяти, внимания, творческого воображения, наблюдательности, последовательности рассуждения и его доказательности, развитию умения кратко, четко и правильно излагать свои мысли.