Формирование действий моделирования на уроках математики в начальной школе при решении текстовых задач

Текстовые задачи являются частью программного курса математики начальной школы, а умение их решать является одним из основных показателей уровня математического развития обучаемых на начальной ступени образования. В процессе решения любой текстовой задачи, учащиеся сталкиваются с необходимость моделировать: как на этапе разбора текста задачи, так и на этапах ее решения и проверки полученного ответа [3].

В процессе решения задачи выделяются три этапа математического моделирования [2]:

1 этап – это перевод условий задачи на математический язык, при этом выделяются необходимые для решения данные и искомые и математическими способами описываются связи между ними;

2 этап – внутримодельное решение (т.е. нахождение значения выражения, выполнение действий, решение уравнения);

3 этап – интерпретация, т.е. перевод полученного решения на тот язык, на котором была сформулирована задача.

Прием моделирования заключается в том, что для исследования какого-либо объекта выбирают (или создают) другой объект, в каком-то отношении подобный тому, который исследуют. Построенный новый объект изучают, с его помощью решают исследовательские задачи, а затем результат переносят на первоначальный объект.

Стойлова Л.П. выделяет следующие типы моделей, рассматриваемые в начальном курсе математики: вспомогательные (схематизированные и знаковые, различающиеся по видам средств, используемых для построения) и решающие (арифметические и алгебраические) [4]. Схематизированные модели, в свою очередь, делятся на вещественные и графические в зависимости от того, какое действие они обеспечивают. Вещественные (или предметные) модели текстовых задач обеспечивают физическое действие с предметами. Они могут строиться из каких-либо предметов (пуговиц, спичек, бумажных полосок и т. д.), и они могут быть представлены разного рада инсценировками сюжета задач. К этому виду моделей причисляют и воссоздание реальной ситуации, описанной в задаче, в виде представлений.

Для формирования действия моделирования С.П. Баранов предложил несколько этапов: замещение, кодирование и декодирование. [1] Замещение является основополагающим этапом в формировании действия моделирования у младших школьников: с помощью знаково-символических средств учащиеся усваивают механизм замещения реального предмета или явления на модель. В результате этого ученики получат образ-заменитель оригинала. В математике выделяют несколько видов образов-заменителей, их можно объединить в несколько групп:

1. Заместители (точки, цветы, фигуры и т.д.).

2. Знаки, обозначающие свойства предметов (фишки, контур фигуры и т.д.).

3. Символы, используемые для замещения отношений (>, <; =; =>; ≠) [5].

На втором этапе − этапе кодирования − происходит переход текстовой информации на язык знаков. Данный этап включает два уровня: графический и вещественный. Для эффективного усвоения детьми действия кодирования педагог может использовать разноплановые операции, с помощью которых дети будут постепенно осваивать данное действие.

1 шаг − преобразование модели, а именно, достраивание модели и удаление лишних элементов.

А) Достраивание модели.

Задача 1. В реке плавало 3 щуки и столько же лещей. Сколько всего рыб плавало в пруду (рис. 1)?

Рисунок 1. Прием достраивания модели

Б) Удаление лишних элементов.

Задача 2. Бабушка приготовила 6 пирожков, а Лена на два пирожка меньше. Сколько всего пирожков они приготовили?

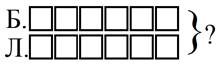
Рисунок 2. Прием удаления лишних элементов

После проведения анализа задачи учащиеся делают вывод, что данная модель не соответствует условиям задачи. Количество фигур, заменяющих пирожки, изготовленные Леной, не соответствует данным задачи. Учащиеся должны убрать или зачеркнуть лишние элементы.

2 шаг − работа по расшифровке модели.

Задача 3. В автобусе может ехать водитель и еще 22 человека. Сколько всего людей может ехать в автобусе? Запишите выражение, соответствующее данной модели (рис. 3).

Рисунок 3. Прием расшифровки модели

3 шаг − видоизменение модели.

При решении задачи: «Бабушка приготовила 6 пирожков, а Лена на два пирожка меньше. Сколько всего пирожков они приготовили?» учащиеся составляют краткую запись (рис. 4), а затем преобразовывают ее в схематическую модель (рис. 5).

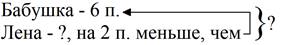
Рисунок 4. Краткая запись

При преобразовании краткой записи в схематическую модель учащиеся показывают количество приготовленных пирожков при помощи отрезков, а вопрос задачи показывается фигурной скобкой.

Рисунок 5. Схематическая модель

4 шаг − усложнение модели.

Например, к задаче «На двух полках было 16 книг. На первой полке было 4 книги. Сколько книг на второй полке?» дается схема, представленная на рис. 6.

Рисунок 6. Схема к задаче

Учащимся нужно перефразировать текст задачи таким образом, чтобы она подходила под схему, представленную на рис. 7.

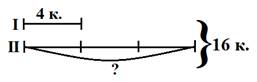
Рисунок 7. Выбор модели

Третий этап − декодирование − приближение модели к оригиналу. На данном этапе используются такие приемы, как:

1) практическое применение модели;

2) использование моделей для описания реальных предметов и явлений;

3) соотнесение результатов моделирования с реальностью;

4) сравнение модели и оригинала.

Приведем пример: в наборе было 10 цветных карандашей. Для рисунка Оля использовала 4 из них. На сколько больше карандашей осталось неиспользованными, чем было использовано? Выберите модель, которая будет подходить к условию данной задачи.

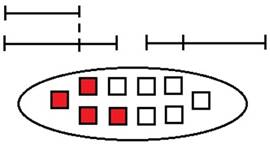
Рисунок 8. Выбор модели

В заключение отметим, что моделирование является одним из самых эффективных инструментов учебной деятельности уже с начальной ступени обучения. Для педагога это инструмент построения учебного процесса, а для ученика это универсальный инструмент основного вида деятельности – обучения. В процессе моделирования у учащихся формируются основные учебные умения, определяющие развитие психологических способностей личности, осуществляющихся в рамках нормативно-возрастного развития личностной и познавательной сфер ребенка.