К вопросу обучения решению текстовых задач в начальном курсе математики
Конференция: XVII Студенческая международная научно-практическая конференция «Гуманитарные науки. Студенческий научный форум»
Секция: Педагогика

XVII Студенческая международная научно-практическая конференция «Гуманитарные науки. Студенческий научный форум»
К вопросу обучения решению текстовых задач в начальном курсе математики
С термином «задача» школьники сталкиваются с первых дней изучения математики. Решая задачи, обучаемые приобретают новые или закрепляют уже имеющиеся математические знания. Задачи выполняют развивающую функцию по отношению к ученикам начальной школы. В процессе решения текстовых задач у школьников отрабатываются умения:
- выполнять операции анализа (разделение задачи на структурные составляющие) и синтеза (соединение целого из частей);
- аргументировано обосновывать свою точку зрения;
- обобщать способы решения типовых задач;
- проводить рассуждения на основе правил логического вывода;
- устанавливать связь теоретических знаний в области математики с жизнью [3].
В связи с этим, важно, чтобы учитель имел глубокие представления о текстовой задаче, о ее структуре, умел решать такие задачи различными способами и мог передать эти знания своим ученикам.
В начальном курсе математики рассматриваются простые и составные задачи. Простой называют задачу, которая решается при помощи одного действия. Например, в одной песочнице играло 7 детей, а в другой на 4 ребенка меньше. Сколько детей играло во второй песочнице?
1) 7 – 4 = 3 (реб.) – играло во второй песочнице.
Ответ: 3 ребенка.
Под составной понимают задачу, в решении которой, в отличие от простой задачи, используют два или более действия.
Например, в автобусе ехали 4 женщины и 5 мужчин. Когда несколько человек вышли, осталось 2 пассажира. Сколько вышло человек?
1) 4 + 5 = 9 (чел.) – было всего пассажиров;
2) 9 – 2 = 7 (чел.) – вышли из автобуса.
Ответ: 7 человек.
В процессе обучения математике в начальной школе, ученики осваивают способы преобразования простой задачи в составную. Так, например, в приведенной выше задаче о песочнице достаточно дополнить ее требованием: преобразуй вопрос задачи так, чтобы она решалась в два действия.
В курсе математики начальной школы особого внимания заслуживают обратные задачи, которые составляются на основании какой-либо имеющейся. В обратных задачах искомые данные уже известны, требуется найти одну из величин, которые были даны в условии исходной задачи. Обратные задачи выполняют функцию проверки решения и самоконтроля школьников. Кроме того, их составление позволяет проверить, насколько ученик верно установил связи между данными и искомыми величинами в задаче.
Задача 1. В магазине килограмм авокадо стоит 120 рублей, а килограмм манго – 150 рублей. На сколько манго дороже авокадо?
Для решения этой задачи нужно найти разность между двумя величинами – стоимостью манго и стоимостью авокадо:
1) 150 – 120 = 30 (руб.).
Ответ: 30 рублей.
При составлении обратной задачи мы используем информацию о разнице в стоимости фруктов, которая составляет 30 рублей. Будем находить либо стоимость авокадо, либо стоимость манго, то есть здесь можно составить две обратные задачи.
Первая обратная задача: килограмм авокадо стоит 120 рублей, а килограмм манго на 30 рублей дороже. Сколько рублей стоит один килограмм манго?
1) 120 + 30 = 150 (руб.).
Ответ: 150 рублей.
Вторая обратная задача: килограмм манго стоит 150 рублей, а килограмм авокадо на 30 рублей дешевле. Сколько стоит один килограмм авокадо?
1) 150 – 30 = 120 (руб.).
Ответ: 120 рублей.
Рассмотренные нами задачи относятся к текстовым. Вспомним, что текстовая задача представляет собой описание реально возможной жизненной ситуации на естественном языке. В таких задачах сформулирован вопрос, на который нужно найти ответ, опираясь на данные задачи.
Теперь, когда мы уже имеем представление о том, какие существуют виды задач, попробуем выяснить смысловую разницу между понятиями «задача» и «текстовая задача». Также рассмотрим на конкретных примерах.
Задача: длина стороны квадрата 6 см. Найдите площадь и периметр квадрата.
Текстовая задача: Егор едет на велосипеде в школу и приезжает через 15 минут. Если известно, что его скорость составляет 15 км/ч, то какое расстояние между школой и его домом?
Таким образом, отличительной чертой текстовой задачи является наличие жизненного сюжета с реальными людьми и событиями.
Несмотря на то, что текстовые задачи приближены к повседневной жизни, у ребенка в младшем школьном возрасте зачастую возникают трудности в их решении, так как у детей на начальном этапе обучения еще слабо развито словесно-логическое мышление. Поэтому при составлении плана решения задачи они используют вспомогательные модели, которые облегчают сам процесс решения. Благодаря вспомогательным моделям, поиск решения задачи становится доступным каждому ребенку. Основными видами моделей, используемыми при решении текстовых задач, являются: рисунок, условный рисунок, чертеж, схема, таблица, краткая запись, блок-схема.
С помощью рисунка ребенок изображает реальные предметы, о которых говорится в задаче, или условные предметы в виде геометрических фигур.
Задача 2. У Виктора 3 карандаша. Мама купила ему набор, в котором 6 карандашей. Сколько стало карандашей у Виктора (рис. 1)?

Рисунок 1. Вспомогательный рисунок к задаче 2
Условный рисунок предполагает замещение изображений реальных объектов геометрическими фигурами (квадратами, кругами, треугольниками и т.д.).
Чертеж – это вспомогательная модель, в которой можно отобразить величины, о которых говорится в задаче и установить между ними реальные отношения.
Задача 3. Катя нарисовала 5 деревьев, а Вова – на 3 дерева больше. Сколько деревьев нарисовал Вова (рис. 2)?
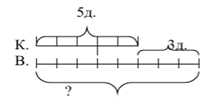
Рисунок 2. Вспомогательный чертеж к задаче 3
Если чертеж предполагает точное отображение существующих в задаче взаимосвязей, то на схематическом чертеже (схеме) школьники условно изображают представленные между величинами отношения (рис. 3).
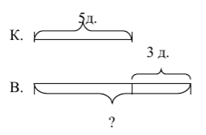
Рисунок 3. Схематический чертеж к задаче 3
Схемы также используются в том случае, когда ученикам необходимо понять отношения, которые достаточно сложно изобразить в точных размерах. Схемы используются в текстовых задачах на движение (встречное движение, движение в одном направлении и в противоположных направлениях) [4].
Задача 4. Из двух городов, находящихся на расстоянии 520 км, одновременно вышли навстречу друг другу два поезда, которые встретились через 4 ч. Один поезд шел со скоростью 60 км/ч. С какой скоростью шел второй поезд?
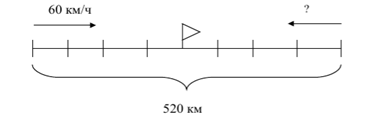
Рисунок 4. Схема к задаче на встречное движение
Таблица – вид вспомогательной модели, который отражает условия задачи в виде строк и столбцов. Обычно таблицы составляют при решении задач на движение, стоимость и работу. Пользуясь такой схемой, нетрудно найти план и осуществить решение задач [1].
Краткая запись – еще один вид вспомогательной модели, который предполагает краткое изложение условий задачи. В краткой записи фиксируются величины, числа – данные и искомые, а также некоторые слова, показывающие, о чем говорится в задаче.
Задача 5. Папа с Володей собирали грибы. Папа нашел 8 грибов, а Володя на 3 гриба больше. Сколько всего грибов нашли Володя и его папа?

Рисунок 5. Краткая запись к задаче 5
Блок-схема представляет собой алгоритм или процесс, где каждое действие показывается с помощью блоков различной формы, которые соединены между собой линиями, указывающими направление алгоритма решения. Блок-схема подразумевает использование индуктивного метода (решение задачи от действия к вопросам) и дедуктивного метода (решение задачи от вопроса к действиям) [2]. Блок-схемы могут использоваться на этапе разбора задачи.





