Использование общей математической карты на уроках математики

Правильно составленная математическая карта способна во многом помочь учителю на уроках планирования изучения нового материала. Карта отражает математическое содержание и структуру предстоящей темы, что способствует вовлечению учащихся в процесс планирования. Так же, математическая карта помогает на уроках систематизации и обобщения изученной темы. Данная статья посвящена способам использования общей математической карты на уроках математики, на примере изучения темы «Делитель и кратное».

Для составления общей математической карты по предстоящей теме, в первую очередь, был проведен анализ математического содержания пунктов учебников по теме «Делитель и кратное». Были проанализированы следующие учебники: Н.Я. Виленкин: Математика. 6 класс [1, с.4–9]; И.И. Зубаревой, И.Г. Мордковича «Математика» 6 класс [4, с.160–167]; С.М. Никольского, М.К. Потапова, Н.Н. Решетникова, А.В. Шевкина «Математика» 5 класс [5, с.143–149]; Гельфман Э.Г. Холодная О.В.«Математика» 6 класс [2, с.34–37], [3, с.6–15, с.154-155 ]. Результатом данного анализа является общая математическая карта отражающая основное математическое содержание темы «Делитель и кратное» представленного в рассмотренных учебниках (Рисунок 1.). Данная карта составлена таким образом, чтобы учащиеся до изучения темы имели представление о ней, и моги быть включены в процесс планирования ее изучения.

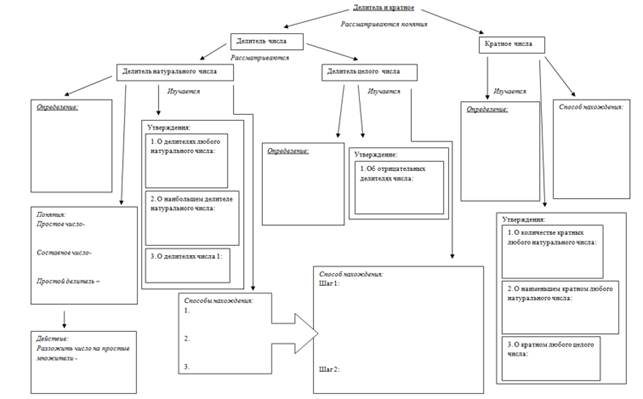
Рисунок 1. Общая математическая темы «Делитель и кратное»

После проведенного анализа школьных учебников математики, были разработаны фрагменты урока планирования изучения темы «Делитель и кратное», урока систематизация и обобщение изученной темы «Делитель и кратное».

Фрагмент 1: Планирование изучения темы «Делитель и кратное».

Цель: составить план по изучению темы «делитель и кратное»; включить учащихся в процесс планирование темы.

Средства: раздаточный материал, компьютерная презентация.

Ход урока:

Учащимся предоставляется раздаточный материал с математической картой (Рисунок 1.) и демонстрируется компьютерная презентация с идентичным содержанием.

·     Ребята, какую тему мы будем изучать на предстоящих уроках?

·     Мы будем изучать тему «Делитель и кратное».

·     Какие понятия рассматриваются в данной теме?

·     В данной теме рассматриваются понятия «делитель числа» и «кратное числа».

·     Какие понятия мы рассмотрим при изучении делителя числа?

·     Мы рассмотрим понятия «делитель натурального числа» и «делитель целого числа».

·     Что мы должны изучить при рассмотрении понятия «делитель натурального числа»?

·     Мы должны изучить определение, утверждения, понятия «простое число», «составное число», «простой делитель», действие разложения числа на простые множители и способы нахождения.

·     Сколько способов нахождения делителей натурального числа мы изучим?

·     Мы изучим три способа нахождения делителей натурального числа.

·     Что мы должны изучить при рассмотрении понятия «делитель целого числа»?

·     Мы должны изучить определение, утверждение, способ нахождения.

·     Что вы можете сказать о способе нахождения делителей целого числа?

·     Способ нахождения делителей целого числа связан со способами нахождения делителей натуральных чисел.

·     Какие утверждения мы должны изучить при рассмотрении понятия «делитель числа»?

·     При рассмотрении понятия «делитель числа» мы изучим утверждения о делителях любого натурального числа, о наибольшем делителе любого натурального числа, о делителе числа 1, об отрицательных делителях числа.

·     Что мы должны изучить при рассмотрении понятия «кратное числа»?

·     Мы должны изучить определение, утверждения и способы нахождения.

·     Какие утверждения мы должны изучить при рассмотрении понятия «кратное числа»?

·     Мы должны изучить утверждения о количестве кратных любого натурального числа, о наименьшем кратном любого натурального числа, о кратном любого целого числа.

Комментарий: Целью использования карты на данном этапе учебного занятия является составление плана по изучению темы. Математическая карта способствует вовлечению учащихся в процесс планирования, позволяет им самостоятельно озвучить основные вопросы предстоящей темы и предварительно ознакомиться с ее содержанием.

Фрагмент 2: Систематизация и обобщение изученной темы «Делитель и кратное»

Цель: обобщить и систематизировать полученные знания по изученной теме «Делитель и кратное».

Средства: заполненная математическая карта (Рисунок 2.), компьютерная презентация.

Ход урока:

Организовать работу на уроке можно с использованием нескольких приемов:

              I.          Прием выстраивания рассказа, когда начало предложения говорит учитель:

·     Мы изучили тему «Делитель и кратное». Рассмотрели понятия …

·      «делитель числа» и «кратное числа».

·     При изучении делителя числа, мы рассмотрели понятия …

·      «делитель натурального числа» и «делитель целого числа».

·     Делителем натурального числа a называют ….

·      (Один из учащихся продолжает фразу, начатую учителем, после чего она появляется на слайде.)

·     Простое число, это число, которое …

·     (Один из учащихся продолжает фразу, начатую учителем, после чего она появляется на слайде.)

·     Составное число, это число, которое …

·     (Один из учащихся продолжает фразу, начатую учителем, после чего она появляется на слайде.)

·     Способами нахождения делителей натурально числа, являются …

·      (Один из учащихся продолжает фразу, начатую учителем, после чего она появляется на слайде.) и т.д.

Данный прием повторяется до тех пор, пока не будет заполненная вся математическая карта (Рисунок 2.).

           II.          Прием, в котором один ученик или цепочка учеников выстраивают рассказ:

·     (Имя ученика), раскрой содержание изученной нами темы.

·     Мы изучили тему «Делитель и кратное». В данной теме мы рассмотрели понятия «делитель числа» и «кратное числа». При рассмотрении понятия «делитель числа», мы изучили понятия «делитель натурального числа» и «делитель целого числа». Делителем натурального числа a называют ….

·     (Одновременно с ответом ученика, посредством анимации, происходит заполнение математической карты на слайде).

Учащийся рассказывает содержание изученной темы или учитель может остановить его и попросить продолжить рассказ другого ученика и т.д. Рассказ продолжается до тех пор, пока не будет заполнена вся математическая карта.

        III.          Прием разбиения учащихся на группы:

Вариант 1:

·     Ребята, распределитесь на группы по n человек. Каждый член группы должен рассказать своим товарищам содержание изученной темы. Через (определенное время выбранное учителем) я опрошу некоторых членов группы. Работайте.

По истечению отведенного учителем времени, учащиеся отвечают содержание изученной темы. Одновременно с их ответами происходит заполнение математической карты посредством анимации.

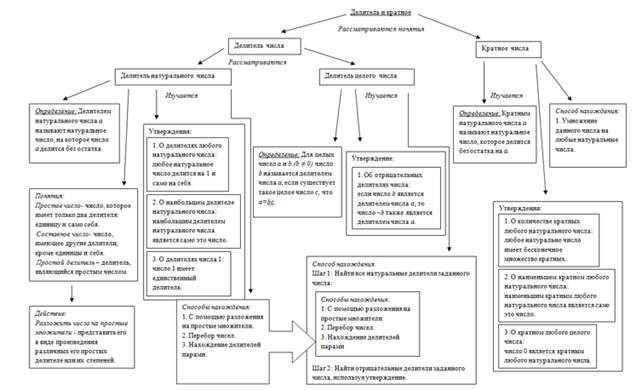
Рисунок 2. Заполненная математическая карта

Вариант 2:

·     Ребята, распределитесь на группы по n человек. От каждой группы потребуется по одному представителю. Каждый из представителей групп вытащит один из жетонов, лежащих на моем столе. После этого, в течении (определенное время выбранное учителем) участники групп на оценку отвечают своим товарищам содержание темы. По истечению времени, я приступлю к опросу групп в соответствии с наименованием жетонов, которые они вытащили. Приступим к выполнению данного задания.

Учащиеся делятся на указанные группы, и выбранные представители поочередно вытаскивают предложенные жетоны. В каждой из групп учащиеся рассказывают друг другу содержание изученной темы, после чего их товарищи выставляют им оценки за ответ. По истечению отведенного времени, учитель приступает к опросу каждой группы в соответствии с наименованием жетонов.

Наименование жетонов:

«Доверие» ‒ учитель выставляет оценки всем участникам группы, вытащившей данный жетон, в соответствии с теми оценками, которые были поставлены их товарищами за ответ.

«Представитель» ‒ группа вытащившая данные жетон, выдвигает одного из своих участников для ответа по выбранной теме. Учитель выставляет оценки всем участникам группы в соответствии с ответом «представителя».

«Жертва» ‒ учитель вызывает любого участника группы для ответа по выбранной теме. Оценки выставляются всем участникам группы в соответствии с ответом «жертвы».

«Все» ‒ учитель вызывает каждого участника группы для ответа. Ответы участников оцениваются независимо друг от друга.

Примечание: Жетоны могут дублироваться в произвольном порядке в зависимости от желания учителя. При опросе групп типа «Все», учитель может пользоваться предложенными выше способами опроса учащихся.

Комментарий: Целью использования карты на данном этапе учебного занятия является обобщение и систематизация полученных знаний учащихся по соответствующей теме. Незаполненная математическая карта является «планам», которым руководствуются учащиеся при выстраивании ответа по данной теме. Грамотно составленная анимированная презентация позволит проверять правильность ответов учащихся во время ответа.

Разработанными фрагментами уроков можно пользоваться в готовом виде, или использовать в качестве примера для составления фрагментов уроков по изучению других тем школьной программы.