Пропедевтика функциональной линии в начальном курсе математики

В статье рассматриваются вопросы пропедевтики изучения функциональной линии в начальной школе; приведены примеры заданий с функциональным содержанием, в результате решения которых происходит формирование представлений о функциональной зависимости у младших школьников.

Пропедевтика функциональной линии является одной из основных дидактических линий начального курса математики, так как она ведет за собой подготовку школьников к изучению систематического курса математики в 5–6-х классах, курса алгебры в 7–9-х классах и основ математического анализа в 10–11-х классах. Главной задачей пропедевтики является развитие общих мыслительных умений, таких как: умение выделять в математических объектах признаки различия и сходства, устанавливать причинно-следственные связи, отличать главное от второстепенного и подводить итог. Особое место в сфере школьного математического образования отводится вырабатыванию понимания, что же такое функция, а также представлению у учащихся основных свойств функций. Так же необходимо понимать, что «функция» обладает глобальностью своих возможностей, позволяющих увязать между собой многие разделы самой математики, так и разделы других школьных дисциплин, например, физики, геометрии и т.д.

В методике обучения функциональному материалу первостепенная роль отводится его пропедевтике в начальной и основной школе до начала систематического изучения понятия функции и ее свойств (способов определения функции [1], способов задания, общих свойств и др.). Подготовительная работа по созданию функциональной базы должна вестись регулярно и систематически через систему всевозможных упражнений, в основе которых лежит идея функциональной зависимости. Эта работа будет способствовать количественному накоплению фактов о зависимостях между величинами и приобретению учащимися опыта соответствующих учебных действий, которые позволят сформировать у них правильные представления, ведущие затем к образованию функциональных понятий, развитию функционального мышления. Подготовительный этап не предполагает сообщения учащимся каких-либо дополнительных сведений к изучаемому программному материалу, а лишь там, где возможно, подчеркивается функциональный момент вопроса. В некоторых учебниках алгебры еще определенное время продолжается функциональная пропедевтика.

Функциональная пропедевтика может осуществляться при рассмотрении следующих вопросов:

1.  Решение текстовых задач, которые предполагают рассмотрение зависимостей между величинами, осмысление простейших правил, закономерностей [2]. Учащиеся постепенно приучаются к тому, что есть величины, которые могут менять свои числовые значения, причем в зависимости от изменения одной величины (например, времени) другая величина (путь) тоже меняется.

Задача 1. Два автомобиля одновременно выехали со стоянки в противоположных направлениях со скоростями 60 км/ч и 70 км/ч. Какое расстояние будет между ними через 1 час? 2 часа? 3 часа?

Задача 2. Из двух городов, находящихся на расстоянии 64 км, одновременно отправились навстречу друг другу два велосипедиста. Один ехал со скоростью 14 км/ч, другой – 18 км/ч. Какое расстояние проехал до встречи каждый велосипедист?

Задача 3. Посыльный катер преодолел расстояние от Североморска до плавбазы подлодок за 8 ч со скоростью 30 км/ч. На обратном пути то же расстояние катер прошел за 6 ч. Какова скорость катера на обратном пути?

Задача 4. Фиксик Симка за 10 часов чинит 6 телевизоров. За какое время она починит 18 телевизоров, если будет работать с той же скоростью?

Задача 5. Велосипедист проехал 90 км за 5 ч. За какое время велосипедист проедет 180 км с такой же скоростью?

2.  Исследование зависимости между результатами арифметических действий и значениями их компонентов. Зависимость понимается здесь в том смысле, что изменение одного или нескольких компонентов (например, увеличение каждого из множителей в 2 раза) приводит к изменению результата (увеличению произведения в 4 раза). Вывод может быть оформлен в виде таблицы, которая наглядно устанавливает характер изменения.

Задача 6. Вычисли 7 – 4 = ? Первое слагаемое увеличилось на 3, как изменилась сумма?

Задача 7. Разность двух чисел уменьшилась на 7. Какие изменения произошли с уменьшаемым?

Задача 8. Заполни таблицу:

Как изменяется разность? С чем это связано?

3.  Буквенные выражения, простейшие тождественные преобразования и числовые значения. Полезно обращать внимание учащихся на то, что значения выражений (например, 4m; 5+a) изменяются от изменения значений букв. Использование таблиц с одним или несколькими выражениями способствует усвоению понятия «соответствующие значения выражений», подчеркивается функциональная природа выражений. Необходимо показать учащимся, что выражение в некоторых частных случаях не имеет смысла (так, например, на нуль делить нельзя). Важно научить их под буквой видеть неизвестное число.

Задание 9. Двое поваров приготовили пиццы. Первый повар работал 6 часов, готовив по 10 пицц в час, а второй 5 часов, готовив по х пицц в час. Сколько всего пицц приготовили повара? Найдите значение полученного выражения при х = 7, 9, 12.

4.  Формулы. Учащиеся знакомятся со смыслом понятия «формула» как равенства, содержащего буквы; различными часто встречающимися формулами из геометрии, физики; учатся сами составлять формулы и производить вычисления по ним. Работая с формулой, они выясняют, от скольких и каких именно других величин зависит обозначенная величина (стоящая в равенстве слева).

Так, в начальном курсе математики, учащиеся знакомятся с такими формулами, как:

·     формула нахождения скорости: , где V – скорость, S – расстояние, t – время;

·     формула нахождения площади прямоугольника: , где S – площадь, a – длина, b - ширина;

·     формула нахождения периметра прямоугольника:  или , где P – периметр, a – длина, b - ширина;

·     формула нахождения периметра квадрата: , где P – периметр, a – сторона;

·     формула нахождения объема прямоугольного параллелепипеда: , где V – объем, a – длина, b – ширина, c – высота;

·     формула деления с остатком: , , где a – делимое, b – делитель, c – частное, r – остаток;

·     формула стоимости: , где C – стоимость, a – цена, n – количество;

·     формула работы: , где A – работа, V – производительность, t – время;

·     формула суммы: , где a – первое слагаемое, b – второе слагаемое, с – сумма;

·     формула разности: , где a – уменьшаемое, b – вычитаемое, с – разность;

·     формула переместительного закона сложения: , где a и b –слагаемые;

·     формула сочетательного закона сложения: , где a, b, и с – слагаемые;

·     формула умножения: a ∙ b = c, где a – первый множитель, b – второй множитель, с – произведение;

·     формула деления: , где a – делимое, b – делитель, с – частное;

·     формула переместительного закона умножения , где a и b –множители;

·     формула сочетательного закона умножения: , где a, b и с – множители;

·     формула распределительного закона умножения:

·     относительно сложения - , где a - первое слагаемое, b - второе слагаемое, с – множитель;

·     относительно вычитания - , где a – уменьшаемое, b – вычитаемое, с – множитель;

5.  Уравнения, которые решаются на основе связи между компонентами и результатами арифметических действий.

Задача 10. Решите уравнение:

·      – для того чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое;

·      - для того чтобы найти неизвестное слагаемое, необходимо от суммы вычесть известное слагаемое;

·      - для того чтобы найти неизвестный делитель, нужно делимое разделить на частное.

6.  Координатная плоскость, которая позволяет наглядно представлять зависимости между двумя величинами. Учащиеся знакомятся с терминологией; учатся определять координаты точек и строить точки по координатам, строить геометрические фигуры и простейшие графики. Школьники осваивают учебные действия по работе с системой координат, которые будут необходимы при изучении конкретных функций.

7.  Диаграммы (круговая, столбчатая), которые наглядно представляют зависимости между дискретными величинами.

Задача 11. На линейной диаграмме показано, сколько различных опытов провели в подводной лодке во время исследования реки Енисей Оля, Катя, Дима, Филипп и доктор Алексеев. Единичный отрезок на диаграмме составляет 1 час.

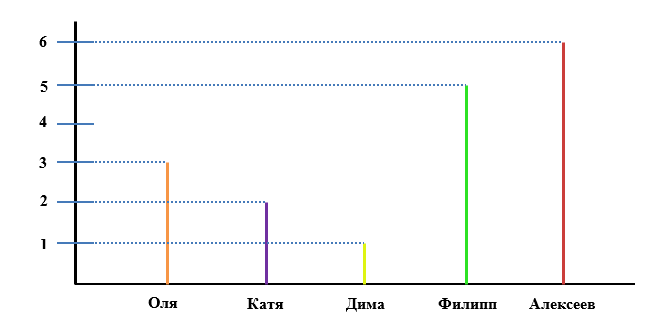
Рисунок 1. Диаграмма распределения количества опытов

Ответьте на вопросы: какое количество опытов провела Оля? Кто больше всех провел опытов? Кто меньше всех провел опытов? Кто провел больше четырех опытов? Кто провел меньше трех опытов? Самостоятельно составьте еще несколько вопросов к данной диаграмме и ответьте на них.