Пример решения задачи линейного программирования

Математическое программирование является разделом математики, который исследует многомерные экстремальные задачи управления и планирования и разрабатывает методы их решения [3].

Математическое программирование ориентировано на решение задач о нахождении минимумов и максимумов функции, области значений аргументов которой ограничены системой равенств (каноническая модель) или неравенств (неканоническая модель). Функция F(x), оптимальное значение которой необходимо найти, называется целевой функцией, а дополнительные условия называются системой ограничения задачи.

Задача математического программирования является линейной, если целевая функция F(x) линейная, а система ограничений состоит из линейных уравнений или неравенств. Раздел математического программирования, описывающий методы решения таких задач, называется линейным программированием. Задача относится к нелинейному программированию, если функция F(x) или хотя бы одно из уравнений или неравенств из системы ограничений нелинейно [1].

Задачи линейного программирования решают широкий круг вопросов планирования экономических процессов, где требуется найти лучшее решение. В качестве целевой функции могут рассматриваться прибыль от реализации, которая должна быть максимальной, издержки производства, которые должны быть минимальными и др.

К экономическим примерам задач линейного программирования относятся: задача производственного планирования, задача о смесях, задача  о раскрое, транспортная задача [3].

Рассмотрим транспортную задачу. Транспортная задача характеризуется тем, что в ней производится перевозка однородного груза из пунктов A к пунктам B, распределенная таким образом, что затраты материальных или временных ресурсов необходимых для доставки минимальны.

Решим пример транспортной задачи. Имеется пять поставщиков сырья, производящих: A1 - 140, A2 - 120, A3 - 110, A4 - 180, A5 - 150 тонн сырья в день. Переработку этого сырья осуществляют три фабрики, перерабатывающих: B1 - 160, B2 - 220, B3 - 170 тонн сырья в день.

Транспортные затраты перевозки сырья от поставщиков до фабрик составляют 300 денежных единиц за тонну на километр. Расстояние от поставщиков до фабрик приведено в таблице.

Таблица.

Расстояние от поставщиков до фабрик, в км

Требуется найти с помощью надстройки «Поиск решения» в Microsoft Excel оптимальное распределение поставок сырья от поставщиков до перерабатывающих фабрик, при котором совокупные транспортные издержки будут минимальны.

Для начала необходимо составить математическую модель. В задаче требуется определить минимальное значение целевой функции:

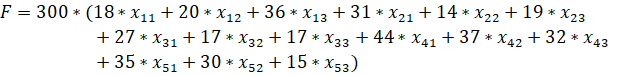
при выполнении условий:

Проверим тип транспортной задачи. Так как сумма объема производства сырья у пяти поставщиков больше, чем производственные возможности трех фабрик переработки, то есть: 140 + 120 + 110 + 180 + 150 > 160 + 220 + 170, то модель задачи открытая, то есть решение найти нельзя. Модель необходимо привести к закрытому типу [2]. Если производится больше сырья, чем потребляется, то необходимо добавить фиктивную фабрику, производственная возможность которой составит (140 + 120 + 110 + 180 + 150) – (160 + 220 + 170) = 150 тонн сырья в день.

После введения фиктивной фабрики задача становится закрытой, и её математическая модель будет иметь вид:

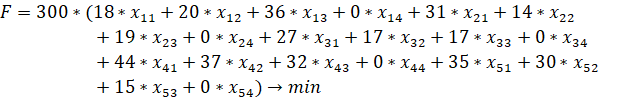
при выполнении условий:

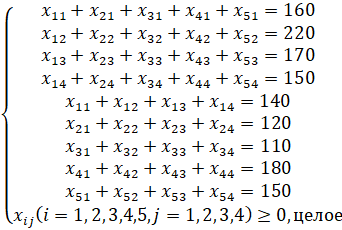
Внесем имеющиеся данные в Excel. В ходе применения надстройки «Поиск решения» в программе должны заполниться значения, характеризующие количество тонн сырья, перевозимое от каждого поставщика к каждой фабрике (от 0 т.). На основе этих сведений заполняются следующие поля: суммарный план перевозки из пунктов производства и оптимальный план перевозок высчитываются как суммы соответствующих ячеек; общая стоимость перевозок (значение целевой функции) определяется как сумма произведений значений расстояния и транспортных затрат (300 д.е.) с объемами перевозок, то есть формула целевой функции примет вид: СУММПРОИЗВ(B4:E8*300; B13:E17) [4]. Результаты поиска решения отображены на рисунке.

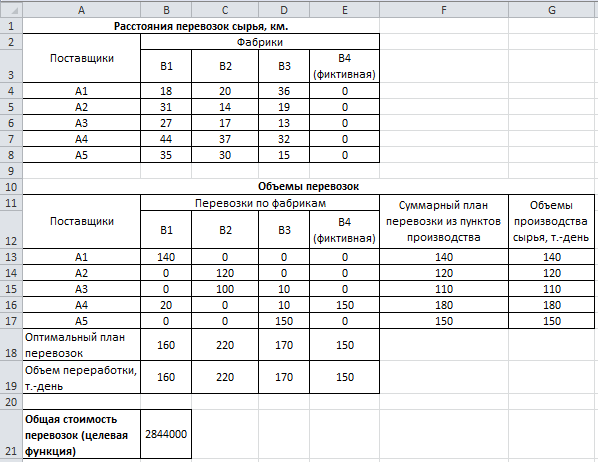
Рисунок. Оптимальное распределение поставок сырья на фабрики

В результате решения задачи была получена минимальная общая стоимость перевозок сырья на фабрики по переработке сырья - 2844000 денежных единиц. При этом перевозка сырья на фабрику B1 осуществляется от поставщиков A1 (140 ед.) и A4 (20 ед.), на фабрику B2 - от поставщиков A2 (120 ед.) и A3 (100 ед.), на фабрику B3 - от поставщиков A3 (10 ед.), A4 (10 ед.) и A5 (150 ед.) и на фиктивную фабрику B4 - от поставщика A4 (150 ед.).

Математическое программирование решает многие экономические задачи, применяемые в разных областях деятельности людей. Транспортные задачи позволяют оптимизировать перевозки груза из одного множества пунктов в другие.