Программная реализация метода правой прогонки при решении линейных систем уравнений

К решению систем алгебраических и трансцендентных уравнений так или иначе сводится три четверти задач прикладной математики, при этом  большую часть из них составляют линейные алгебраические системы, имеющие единственное решение.

Решение задач, связанных с экономикой, физикой, химией и другими науками, в большинстве случаев связано с решением систем линейных уравнений (СЛУ). Их решение является одной из ключевых задач вычислительной линейной алгебры, а также элементарным шагом соответствующего алгоритма при решении различных задач численных методов. Так как задача решения СЛУ является очень важной и практически значимой, многие математики до сих пор обращают на это особое внимание и пытаются разработать более удобные методы решения.

Для решения линейных систем достаточно хорошо известные методы Крамера и Гаусса, а также разработана общая теория. Но по сей день на практике возникает множество различных проблем при решении задач, сводящихся к решению систем линейных уравнений. 

Данные методы имеют свои недостатки. Например, недостатком метода Крамера является то, что он слишком трудоёмкий и пользоваться им практически невозможно. С объёмом таких громоздких вычислений не может справиться даже компьютер.

Метод Гаусса менее трудоёмкий. Тот факт, что количество арифметических операций, необходимых для решения линейной системы n-го порядка методом Гаусса, значительно меньше, позволяет использовать данный метод достаточно широко. Но при решении систем высокого порядка применение метода Гаусса становится проблематичным.

На практике нередко возникают плохо обусловленные системы, для которых характерно быстрое нарастание вычислительной погрешности результата, связанное с округлениями, при увеличении порядка системы. Решение таких систем, даже при небольших порядках, вызывает трудности. Существует достаточное количество методов, позволяющих решать такие задачи. Выделяют следующие группы методов: прямые (методы Гаусса, Жордана, квадратного корня и т.п.) и итерационные методы (методы простой итерации, Зейделя, релаксации  и т. п.).

Кроме перечисленных методов используются специфические методы прогонки – прямые методы, которые по существу представляют собой модификации метода Гаусса и предназначены для решения систем высокого порядка с сильно разреженными матрицами. Эти матрицы состоят в основном из нулей, а ненулевые элементы в них образуют определенные структуры. Подобные системы часто порождаются разностными и проекционными методами. Применительно к решению краевых задач для дифференциальных уравнений методы прогонки очень эффективны.

Метод правой прогонки используется для решения СЛУ с трёхдиагональными матрицами. Он представляет собой модификацию метода Гаусса. Трёхдиагональная матрица – это матрица, на главной диагонали которой находятся лишь элементы отличные от нуля, а остальные должны быть равны нулю.

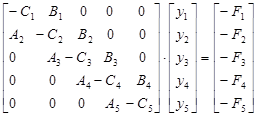                                                                                                               (1)

Рассмотрим СЛУ 5 порядка (рис.1). Отличные от нуля коэффициенты, стоящие на главной диагонали, обозначены  буквой С со знаком минус, а коэффициенты, стоящие на двух соседних диагоналях,  обозначены буквами  А и В соответственно  [3]. Достоинством данного способа является значительная экономия памяти ЭВМ, так как она не тратится на бесполезные нули. Для того, чтобы при решении различных других задач матрицы системы имели одинаковый вид, необходимо перед коэффициентами С и правыми частями F поставить знак минус.

Используя описанную систему обозначений, запишем произвольную систему с трёхдиагональной матрицей (М-1)-го порядка в общем виде:

                                                                                                (2)

При М=6 системы (1) и (2)  эквивалентны. После использования процедуры прямого хода метода Гаусса к решению системы (2), получится система, матрица которой будет иметь две диагонали: главную и правую. Для того чтобы получить систему с двухдиагональной матрицей, на главной диагонали которой стоят единицы, необходимо каждое уравнение преобразованной системы разделить на диагональный элемент, стоящий в этой строке.  Система будет выглядеть следующим образом (при M=6):

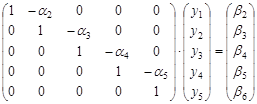                                                                                                                    (3)

А рекуррентные формулы обратного хода метода Гаусса примут вид

             ,                                                                         (4)

причём          .                                                                                                       (5)

Для определения коэффициентов  и  необходимо заменить в равенстве (4) величину m на m-1:

                                                                                           (6)

и  подставить  в (2):

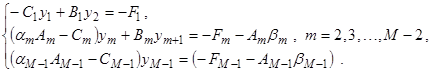
В результате получим:

После сравнения формул с (4), получим: ,      

                                                                                 (7)

Вводятся фиктивные величины     и  .

Пусть  ,                                                                                   (8)

тогда формулы неизвестных коэффициентов  и  при всех допустимых значениях m можно будет записать одинаково:

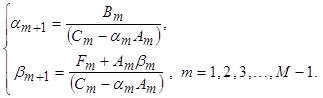                                                                           (9)

Формулы (8) - (9) дают возможность вычислить все неизвестные коэффициенты  и . Чтобы получить решения системы (2) используем рекуррентную формулу (4), но сначала необходимо знать значение . Так как   (так как  ), значение  можно выбрать любое, например,    

                                                                                                            (10)

После проделанных действий получим алгоритм решения системы (2).

Сначала по формулам (9) с начальными условиями (8) получаются значения .  Затем по формуле (4) с начальным условием (10) получается решение системы: .

В процессе вычисления  величин  и  по формулам (9) происходит деление на величины, которые могут обращаться в ноль [3]. В данном случае этот метод не применим. Следовательно, важно знать и заранее проверять условия, при которых можно использовать метод прогонки. Достаточные условия применимости метода прогонки представлены в виде следующей теоремы.

Теорема 1. Если       

, ,  , ,

, , , ,

то  для  следовательно данный метод можно использовать [3].

Описанный выше метод прогонки  реализован в виде программы, часть кода которой представлена ниже:

eps[0]=-A[0][1]/A[0][0];

et[0]=B[0]/A[0][0];

for(i=1;i<n;i++){

    z=A[i][i]+A[i][i-1]*eps[i-1];

    eps[i]=-A[i][i+1]/z;

    et[i]=(B[i]-A[i][i-1]*et[i-1])/z;}

X[n]=(B[n]-A[n][n-1]*et[n-1])/(A[n][n]+A[n][n-1]*eps[n-1]);

for(i=n-1;i>=0;i--)

    X[i]=eps[i]*X[i+1]+et[i];       

  for(int j=0;j<aj;j++){

 dataGridView3->Rows[j]->Cells[0]->Value=X[j]; } }

Программа предназначена для решения систем линейных уравнений методом прогонки и составлена для матриц различного порядка путем добавления и удаления столбцов на форме (рис.1.). При нажатии на кнопку “Добавить столбец”, программа автоматически добавляет новый столбец в таблицу А, а при нажатии кнопки “Удалить столбец” программа, соответственно, удаляет его. 

На форме (рис. 1.) помимо вышеназванных текстовых полей имеется также поле “Найти Х”. Данное текстовое поле предназначено для нахождения значений столбца Х. Процедура ввода осуществляется следующим образом: наводится курсор на поля и вводятся соответствующие значения. Затем нажимается кнопка “Найти Х”, и  в полях столбца Х появляются значения вектора .

Для того чтобы начать работу с программой, представленной на рисунке (рис. 1.), следует запустить программу, далее в поля таблицы А ввести элементы матрицы.  Благодаря встроенным кнопкам мы можем изменять количество столбцов таблицы. В поля, предназначенные для В, вводятся значения элементов вектора b. Далее нажимается кнопка “Найти Х”.

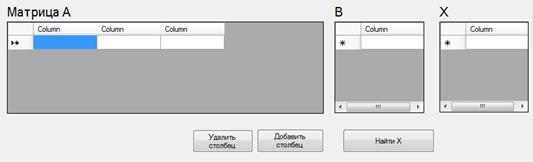
Рисунок. 1. Интерфейс программы «Метод прогонки»

В результате в столбце Х появятся значения решения системы (рис.2.).

Рисунок. 2. Выполнение программы «Метод прогонки»

Следует обратить особое внимание на случай, когда происходит деление на 0. Тогда программа выдаст следующее сообщение (рис.3.).

Рисунок. 3. Сообщение об ошибке программы «Метод прогонки»

Программа производит вычисления по методу прогонки и выводит значения в поля, предназначенные для вывода найденных неизвестных ранее значений вектора .

Для тестирования программы была подобрана система с известным решением. Система с матрицей  и вектором  имеет точное решение - вектор В программу задавались соответствующие исходные данные и были получены результаты. Результаты работы программы приведены на рисунке (рис. 2.).

Чтобы полностью убедиться в том, что программа работает исправно, протестируем ее ещё на одном примере, когда происходит деление на 0. В программу задаются значения матрицы. После ввода матрицы А в поля, предназначенные для В, вводятся произвольные значения элементов вектора b. Далее нажимается кнопка “Найти Х”.

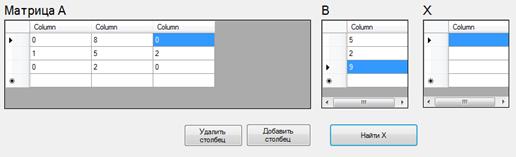
Рис. 4. Выполнение программы «Метод прогонки» при делении на 0

В результате в столбце Х не появятся значения решения системы, а на экран выведется сообщение об ошибке (рис.3.).