Модель Фрейер как способ представления учебной математической информации

В настоящее время важнейшим умением обучающихся становится способность обрабатывать информацию с высокой интенсивностью и эффективностью. Так, в ходе изучения нового материала по математике возникает необходимость его обобщения и структурирования. Для этого, используются различные методы, средства, приемы, которые позволяют обработать большой объем символьной и знаковой информации, и представить ее в новой наглядной форме. В этой связи становится актуальным поиск и адаптация новых средств, способов структурирования теоретического материала. Особенности и возможности информационных моделей позволяют предположить, что данный инструмент будет эффективным средством обобщения содержания обучения математики.

В ходе написания выпускной квалификационной работы было проведено исследование посредством применения программы «Google Формы». В нем приняло участие более 50 респондентов, являющихся учителями математики из разных городов России. Исследование показало следующие результаты.

Более 94 % опрошенных подтвердили тот факт, что запоминание и усвоение математических понятий, фактов и утверждений, представленных с помощью зрительно воспринимаемых форм, происходит качественнее и быстрее, чем представленных в словесной форме. В учебном процессе информационные модели учителя преимущественно используют около двух раз в месяц. Таких респондентов оказалось на 7% больше, чем тех, кто использует информационные модели 3-4 раза в неделю. Такой показатель характеризует информационные модели как актуальное средство для обучения математике. Также опрос показал, что чаще всего учителя применяют кластеры и таблицы (более 80%). Менее используемыми моделями являются опорные конспекты, диаграммы. Большинство респондентов применяют на уроках готовые модели (69,2%).

Важно отметить, что учителя математики удовлетворены наглядностью содержания используемых пособий. Применение информационных моделей, по мнению большинства, способствует повышению качества и индивидуализации обучения. Главным плюсом использования информационных моделей респонденты определили возможность в краткие сроки обобщить и структурировать пройденный материал, что подтверждает практическую значимость исследуемых моделей.

В данной статье рассмотрим один из видов информационных моделей – модель Фрейер. Исследование показало, что данную модель применяют 30,8 % учителей математики.

В педагогических исследованиях модель Фрейер определяется одной из эффективных моделей представления учебной математической информации. Так, Фирер А.В. в своих работах определяет данную модель, как «… обучающая структура, помогающая обучающимся глубоко понять и осознать изучаемый термин или понятие в концепции» [1].

Основная дидактическая функция модели Фрейер – введение и закрепление понятий. Для создания этой модели используется лист бумаги формата не меньше А4, разделенный на 4 равные части, в центре которого располагается рассматриваемый термин.

Структура модели Фрейер (рис. 1):

• левый верхний угол – существенные характеристики понятия;
• правый верхний угол – несущественные характеристики;
• левый нижний угол – примеры объектов, входящих в объем понятия;
• правый нижний угол – контрпримеры (примеры объектов, не входящих в объем понятия).

Рисунок  1. Структура модели Фрейер

Модель Фрейер позволяет акцентировать внимание на различные когнитивные стили учеников. Блоки аналитическая модель и существенные признаки соответствуют когнитивным стилям школьников, характерным для левополушарного доминирования, тогда как присутствие целостного образа понятия, подкрепленного графическими изображениями, учитывает когнитивные стили, характерные для правополушарного доминирования.

Ниже представлен пример модели Фрейер по теме «Функция 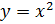» (рис.2). Данная модель разработана для обучающихся 8 класса.

При изучении темы «Функция 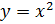 и ее график» представленная модель Фрейер позволит ввести понятие функции вида 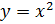, рассмотреть ее существенные признаки, виды графиков и их визуализированные образы. Также применение данной модели позволит принять во внимание когнитивные стили школьников. Аналитическая модель будет соответствовать обучающимся с левополушарным доминированием. Целостный же образ понятия с его графическим представлением будет учитывать особенности школьников с правополушарным доминированием.

Модель Фрейер дает одновременное описание понятия в разных видах, что позволяет построить процесс открытия понятия для обучающихся более полным. Любая модель создается благодаря имеющейся у ученика информации об изучаемом объекте или понятии. Умение создавать модели, как и в целом возможности в познании объектов и явлений, зависит от умения человека правильно понимать, обрабатывать и представлять информацию.

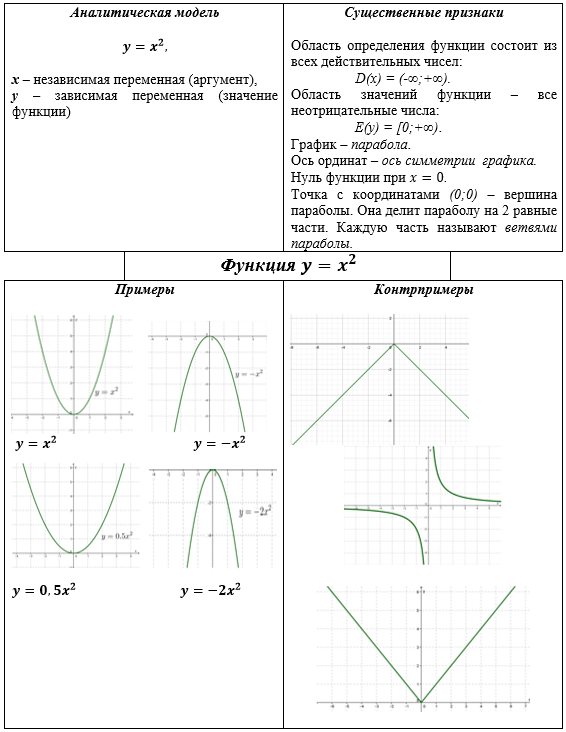
Рисунок 2. Модель Фрейер по теме «Функция 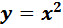 и ее график »