Теория графов в оптимизации программного кода PYTHON
Секция: Физико-математические науки

XXXVIII Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Теория графов в оптимизации программного кода PYTHON
Введение
В современном мире под высоким темпом развития прикладных технологий, поколению, оканчивающему школы и поступающему в университеты на IT специальности, необходимо всё быстрее и быстрее осваивать тот опыт человечества, который формировался в этой сфере десятилетиями. И даже в случае, когда ученик аксиоматически узнаёт новый метод проектирования кода или различных систем, имеет место банальная наработка уместного применения данного навыка при решении практических задач. А учитывая актуальность дистанционного, а иногда и самостоятельного обучения, возникает потребность оценки и проверки суждений ученика при решении практических задач, для их возможной корректировки, что не всегда возможно со стороны преподавателя.
В данной научно-исследовательской работе рассмотрен метод, позволяющий автоматизировано анализировать программный код на языке программирования Python на предмет выполнения и реализации основной парадигмы программирования.
Данный метод актуален в связи с тем, что по мнению специалистов, язык программирования Python идеально подходит в качестве первого изучаемого языка программирования, так как является простым и интуитивно понятным. А, в свою очередь, дублирование кода считается ошибкой новичков. Таким образом, уясняя на примере этого языка данный подход, свойственный всем языкам программирования, имеем более глубокое понимание процессов и идей проектирования кода.
Цель работы
Разработка метода повышения эффективности обучения для начинающих программистов на языке Python
Задачи работы
- Сформулировать самую часто нарушаемую парадигму проектирования кода обучающихся языкам программирования (ЯП);
- Ввести определение графовой модели кода;
- Определить отображение правила написания кода на полученные графовые модели;
- Реализовать алгоритм идентификации дефекта кода [4] и уведомления пользователя об этом.
Основная нарушаемая парадигма проектирования кода на Python
Недопустимость дублирующего кода
Проблема: решая одну и ту же задачу в разных местах кода, во-первых, сложнее проследить правильность выполнения кода, а во-вторых, при необходимости внести изменения в данный алгоритм придётся вносить изменения в его каждый экземпляр.
Решение: централизованное определение данного алгоритма в виде функции либо цикла, с последующими вызовами первой в местах, где это требуется.
Графовая модель кода
Ориентированный, односвязный граф G=(V,E), где V – конечное множество синтаксических конструкций языка и данных, E – конечное множество раскрашенных рёбер.
У рёбер имеется различный приоритет, далее приводятся приоритеты в порядке убывания его значения:
- вызов функций – оранжевый;
- цикличные действия – синий;
- действия по выполнению условия – зелёный, по невыполнению – красный;
- переход от команды к команде в порядке очерёдности – серый.
Определение отображения правила написания кода на полученные графовые модели
Задача нахождения повторов участков кода в программе, при переходе к графовой модели преобразуется в задачу нахождения двух и более максимальных по количеству вершин подграфов в построенной графовой модели, каждая вершина из которых имеет однозначное отображение с допустимым лексическим расстоянием.
Пример:

Рисунок 1. Код, реализующий поиск минимума из первого списка «list_1», максимума из второго «list_1» и вывод получившихся значений на экран
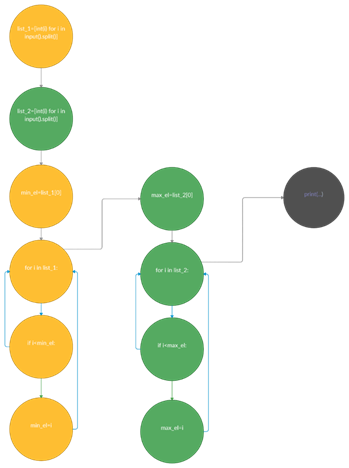
Рисунок 2. Графовая модель, построенная по коду с рис. 1
Совокупность вершин, обозначенных одним цветом, представляют собой сегмент. В данном случае наблюдаем явный повтор схожих конструкций для «зелёного» и «жёлтого» сегментов.
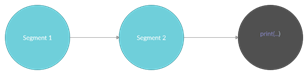
Рисунок 3. Упрощение графовой модели с рис. 2
Для устранения дублирующего кода вводим функцию «Function». Описанная лишь единожды она – вызывается с различными параметрами в «Segment 1» и «Segment 2».
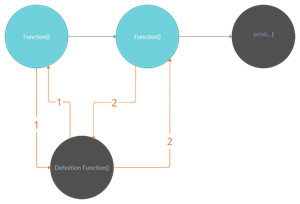
Рисунок 4. Предложение по оптимизации кода с рис. 1
Описание предлагаемого алгоритма
Имея графовую модель исходного кода, находим схожие вершины, помечаем их одним цветом и переносим в новый граф, сохраняя отношения между ними (кроме серых).
Анализируем получившиеся компоненты на предмет участия в решении одной локальной подзадачи, при наличии таковых – объединяем их в одну.
Получив такое разбиение, можем перейти к анализу получившихся графов и поиску максимальных общих подграфов [3]. Анализируя полученные подграфы приходим к выводу, либо о соответствии кода заданному правилу, либо о необходимости произвести рефакторинг, с конкретным указанием участков кода для этого.
Предлагаемый алгоритм
I.Исходный граф представить в виде графовой модели
II.Используя модифицированный поиск [1 с. 10], находим схожие вершины и составляем новый граф:
a.В качестве начальной вершины выбираем исток;
b.Ищем непомеченные вершины, с которыми начальная будет иметь допустимое значение лексического расстояния;
c.При нахождении такой вершины, помечаем её, и копируем в новый граф, причём копируются так же рёбра (корме серых), ведущие к этой вершине из уже присутствующих в новом графе вершин;
d.Делаем очередную вершину начальной, согласно алгоритму обхода в глубину;
e.Повторяем шаги (b-d) до завершения алгоритма обхода в глубину;
III.В получившемся графе проводим анализ на предмет логической связности различных компонент:
a.Находим компоненту, содержащую наименьшее количество вершин;
b.Перебором осуществляем поиск схожей морфемы (например, имени используемой переменной), со всеми остальными не закрытыми компонентами, здесь имеем 3 случая: 1) совпадений не найдено, в таком случае её пометить как закрытую 2) одно совпадение – присоединить эту компоненту к той, в которой найдено совпадение 3) несколько совпадений – присоединить ко всем. Важно присоединение производить в порядке, в котором данные компоненты добавлялись в новый граф;
c.Повторяем шаги (а-b) до тех пор, пока не получим граф с множеством закрытых компонент.
IV.Применить алгоритм нахождения максимального общего подграфа между всевозможными компонентами, например, модифицированный алгоритм Хансера [2, c.10];
V.Если такие подграфы найдены, то код не удовлетворяет принципу отсутствия дубликатов, соответственно именно эти подграфы стоит отметить в качестве цели для оптимизации.
Демонстрация алгоритма
Рассмотрим для наглядности всё тот-же код с рис. 3 и соответствующую ему графовую модель с рис. 2.

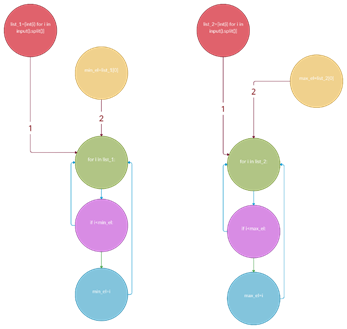
|
Рисунок 5. Новый граф, получившийся после установления в нём логических связей в шаге III |
Рисунок 6. Результат шага IV, наблюдаем 2 подграфа, что говорит нам о наличии дублирующего кода |
Достоинства алгоритма
Главным достоинством данного алгоритма является возможность его программирования и применения для учебных целей при обучении ЯП Python и масштабирования на прочие языки программирования при замене триггеров и правил обработки выражений.
Выводы
В данной работе излагается алгоритм, позволяющий детектировать наличие основной причины запутанности кода у начинающих программистов, что позволит, при программной реализации данного алгоритма, повысить эффективность кода у тех учеников, у которых затруднён или отсутствует доступ к экспертной оценке разрабатываемого кода.





