Покрытия в графах и их практическое применение

Аннотация. В данном исследовании рассмотрим такое направление теории графов различные покрытия и попробуем использовать их при решении практической задачи на примере независимых и доминирующих множеств.

Теория графов – область дискретной математики, основные постулаты которой были разработаны еще в 1763 году известным математиком Леонардом Эйлером, но до определенного момента она считалась скорее развлечением для любителей головоломок. С зарождением кибернетики и затем информатики, ученые поняли, что теория графов достаточно полезна при решении различных прикладных задач.

Граф G=(V, E) – абстрактная математическая модель, состоящая из множества вершин V, которые связаны ребрами из множества Е.

Независимым множеством вершин (либо внутренне устойчивым множеством) назовем такое подмножество множества всех вершин графа V, что  любая пара вершин из того подмножества не смежна. Независимое множество называется максимальным, если не существует другого независимого множества, в которое бы оно входило. Максимальное независимое множество с наибольшим количеством элементов назовем наибольшим. Количество элементов такого множества принято называть числом независимости графа, либо его неплотностью.

К понятию независимости близко понятие доминирования. И доминирующим множеством графа будет являться такое подмножество V1 множества V вершин графа, что любая вершина не вошедшая в V1 смежна с какой-либо вершиной из V1. Доминирующее множество назовем минимальным, если никакое его собственное подмножество не является доминирующим. Минимальное доминирующее множество с наименьшим числом элементов классифицируют как наименьшее, а количество элементов в нем называют числом доминирования графа.

Метод Магу для нахождения независимых множеств

Пусть задан граф G=(V,E), A=(a_ij) – его матрица смежности и S – максимальное независимое множество вершин.

С каждой вершиной графа v_i свяжем булеву переменную

x_i = 1, если  x_i∈S,

x_i = 0,если  x_i ∉S.

Заметим, что если (v_i, v_j)∈E, то либо v_i∉S, либо v_j∉S, либо одновременно v_i, v_j∉S. А значит для всех i, j=1,n, таких что a_ij≠0 истинно высказывание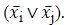 

Учитывая конечность графа:

Преобразуем правую часть выражения к дизъюнктивной нормальной форме с помощью основных равносильностей алгебры высказываний:

xy = yx,  x∨y = yvx - коммутативность;

xx = x,  x ∨ x = x - идемпотентность;

x( y ∨z) = xy ∨ xz,  x(y ∧ z) = xy ∧ xz - дистрибутивность;

x ∨ xy = x - поглощение.

Получим: 

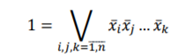
Данное высказывание истинно и позволяет сделать выводы о наборах вершин графа, не входящих одновременно в максимальные независимые множества вершин. Следовательно, получаем информацию о вершинах, образующих максимальные независимые множества.

Метод Магу для нахождения доминирующих множеств

Пусть теперь задан граф G=(V,E), A=(a_ij) – его матрица смежности и T – минимальное доминирующее множество вершин. Тогда для произвольной вершины v_i∈V должно выполняться одно из двух условий (или оба одновременно):

1) вершина v_i принадлежит множеству T;

2) существует некоторая вершина v_j∈T, что (v_j,v_j)∈E

Если с каждой вершиной связать булеву переменную

х_i  = 1, если   х_i ∈T,

х_i  = 0, если  х_i  ∉T.

то будет справедливо высказывание

Учитывая конечность графа:

Преобразовывая правую часть к дизъюнктивной нормальной форме, получим информацию о минимальных доминирующих множествах графа.

Пример нахождения независимых и доминирующих множеств

Рисунок 1. Пример графа

Поиск максимальных независимых множеств:

Для графа рис.1 составим истинное высказывание:

1 = (x₁ + x₂)( x₂ + x₃)( x₂ + x₅)( x₄ + x₁)( x₄ + x₃)( x₄ + x₅)

Заметим, что число конъюнктивных множителей равно количеству ребер графа. Преобразуем его к дизъюнктивной нормальной форме:

1 = [( x₁ + x₂)( x₂ + x₃)][( x₂ + x₅)( x₄ + x₁)][( x₄ + x₃)( x₄ + x₅)] = x₁ x₃ x₅ + x₂ x₄

Делаем вывод о наличии в графе двух максимальных независимых множеств, причем первое НЕ содержит вершины v1,v3,v5, а значит состоит из вершин v2 и v4. Второе – НЕ содержит вершины v2,v4, а значит состоит из вершин v1,v3 и v5.

Таким образом, максимальные независимые множества – {v1,v3,v5}, {v2,v4}.

Поиск минимальных доминирующих множеств:

Для графа рис.1 составим истинное высказывание:

1 = (х₁ + х₂ )( х₂ + х₃ + х₅ ) х₃ ( х₄ + х₁ + х₃ + х₅ ) х₅

Заметим, что число конъюнктивных множителей равно количеству вершин графа.

Преобразуем его к дизъюнктивной нормальной форме :

1=( х₁ + х₂)( х₂ + х₃ + х₅) х₃ ( х₄ + х₁ + х₃ + х₅) х₅ = х₁ х₃ х₅ + х₂ х₃ х₅

Таким образом, в графе существует два минимальных доминирующих множества – {v1,v3,v5} и {v2,v3,v5}

Программное обеспечение

На основании описанного выше алгоритма Магу было разработано программное обеспечение для нахождения независимых и доминирующих множеств.

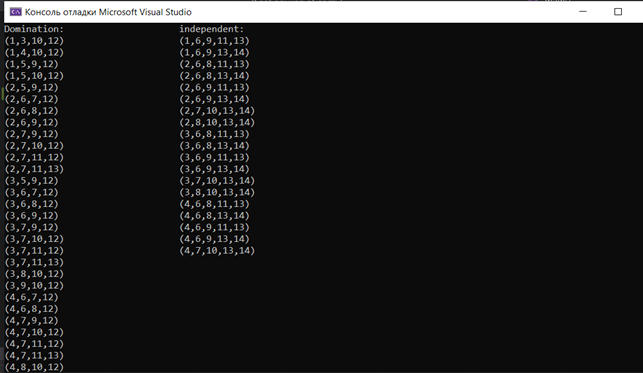
Рисунок 2. Результат выполнения программы

Практическое применение

Для эксперимента был взят восточный округ города Тюмень и по его карте был составлен граф.

При составлении графа использовались следующие правила:

1. Вершинами графа являются входящие в выбранный округ районы.

2. Ребро соединяет вершины только в том случае, если соответствующие им районы находятся на общей границе друг с другом.

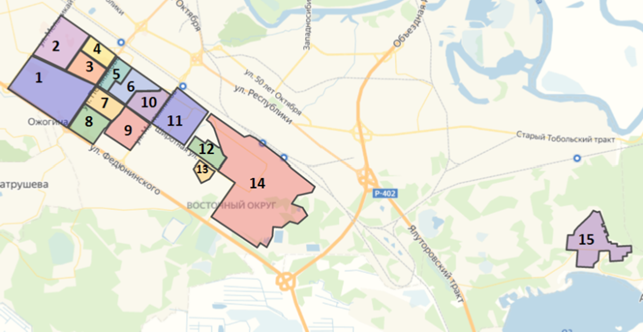
Рисунок 3. Карта Восточного округа г. Тюмень

По данной карте был составлен граф(см. Рисунок 4). Следует отметить, что был исключен из рассмотрения район, обозначенный на нашей карте как 15, так как было выяснено, что он является новообразованным и малонаселенным, из чего был сделан вывод о его незначительности в рамках данного исследования.

Рисунок 4. Граф Восточного округа г.Тюмень

Как мы применили доминирующие множества

Выдвигаем предположение, что в вершинах, соответствующих одному из найденных доминирующих множеств обязательно должны находиться выбранные нами для исследования учреждения. Приступим к проверке предположения.

Рассматриваем расположение школ:

Рисунок 5 позволяет наглядно показать, где именно расположены школы (соответствующие районы выделены красным). Как можно видеть районов со школами гораздо больше 4-х, что в свою очередь больше любого из найденных нами доминирующих множеств.

Делаем вывод об очень удобном местонахождении школ для любого района выбранного округа.

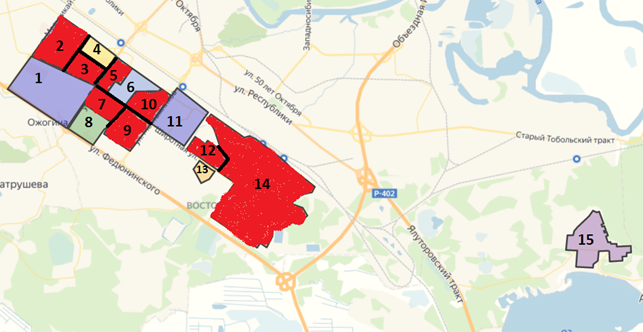
Рисунок 5. Расположение школ

Рассматриваем расположение детских садов:

Ситуация с детскими садами даже лучше, чем со школами. Из Рисунка 6 видим, что единственный район, который не имеет своего детского сада — это 14-й (выделен черным). Такая ситуация кажется нелогичной, потому что как мы видим этот район один из самых крупных. Однако с точки зрения доминирующих множеств существующее расположение детских садов более чем достаточно.

Рисунок 6. Расположение детских садов

Рассматриваем расположение больниц:

С больницами ситуация интереснее. Как нам позволяет увидеть Рисунок 6 количество районов с больницами (выделены красным) не имеет такого значительного превосходства как в случае со школами и детскими садами. Наблюдаем существование больниц в «вершинах» (2,7,9,11,14), что не соответствует ни одному из найденных нами доминирующих множеств, самым близким из которых является (2,7,9,12). Однако при более детально рассмотрении приходим к выводу, что такое существующее расположение более оптимально с точки зрения количества жителей в этих районах

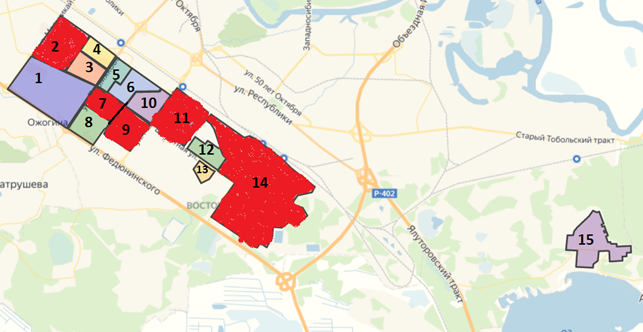
Рисунок 7. Расположение больниц

На основании рассмотренных выше примеров делаем выводы:

1. Расположение школ и детских садов является весьма сбалансированным и удобным для жителей выбранного округа. Практически каждый из районов имеет в своем распоряжении упомянутые учреждения и можно сказать, что добраться до них не составит труда.

2. При исследовании расположения больниц были получены неожиданные результаты, но более тщательный анализ позволяет сказать, что путь до одного из медицинских учреждений также не доставит проблем для жителей выбранного округа.

Как мы применили независимые множества

Ответ на вопрос применимости таких множеств не лежит на поверхности, как в случае с доминирующими. Однако мы попытались использовать полученные результаты для планирования многоэтажной застройки в городе. Так так вершины(районы) в полученных независимых множествах не смежны(не имеют общих границ), то в этих районах можно строить многоэтажные дома с большим количеством жильцов. По нашему мнению постройка таких жилых домов в найденных нами районах не создаст проблемы перенаселения, дорожной перегруженности и дефицита жизненно важных центров обслуживания, так как смежные районы будут при этом заселены относительно негусто, что позволит избежать перечисленных выше проблем.

Рисунок 8 в соответствии с нашими вычислениями как раз показывает один из вариантов расположения многоэтажных жилых домов(выделено зеленым), который не создаст препятствий для комфортной жизни в городе.

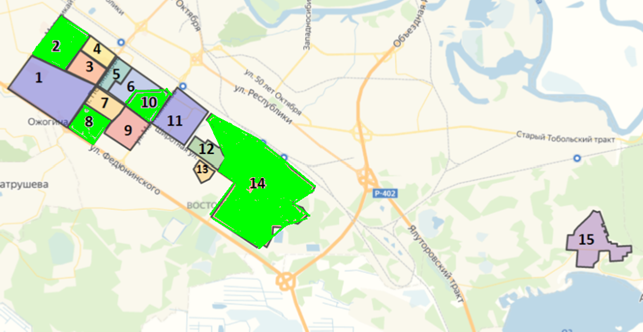
Рисунок 8. Пример расположения многоэтажек

Заключение

Из всего вышесказанного можно сделать вывод, что такой инструмент как покрытия при исследовании различных объектов, если их удается представить в виде графа, может быть достаточно полезен и практичен. Однако сейчас такой подход мало где применяется, так как в нашей интерпретации он недостаточно совершенен. Необходимо учитывать несколько факторов. Например, престиж и качество услуг при применении доминирующих множеств, или историческое наследие и геологическую обстановку для независимых. Но несмотря на это метод довольно перспективный и требует только дальнейшего совершенствования для большей эффективности.