Исследование прочности, деформативности и трещиностойкости изгибаемых железобетонных элементов разного сечения
Секция: Технические науки
лауреатов
участников
лауреатов


участников



XXXIX Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Исследование прочности, деформативности и трещиностойкости изгибаемых железобетонных элементов разного сечения
Аннотация. Рассматриваются различные сечения фиброжелезобетонных балок. В качестве исследуемых балок были использованы балки 4-х типов: три типа – образцы трапециевидного сечения и один тип – прямоугольного поперечного сечения.
Ключевые слова: фиброжелезобетон, прочность, деформативность, трещиностойкость, изгиб.
В качестве исследуемых балок были использованы балки 4-х типов: три типа – образцы трапециевидного сечения и один тип (эталонный) – прямоугольного поперечного сечения. В процессе исследования варьировались классы бетона (В15) и арматуры (А400, А500, А600), а также коэффициент армирования µ в интервале от 0.5 до 5% с шагом 0.5%.
Все исследуемые балки имели постоянную высоту (400 мм), длину пролета (4500 мм) и площадь поперечного сечения, что в свою очередь позволяет дать анализ эффективности распределения материала по высоте сечения без использования приведенных характеристик. Балки были нагружены равномерно распределенной нагрузкой. Геометрические размеры балок приведены на рисунке 1.
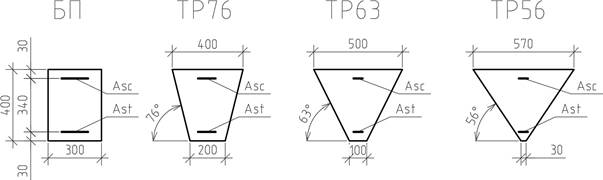
Рисунок 1. Геометрические размеры сечений исследуемых балок
Рассмотрим характер роста прочности при увеличении коэффициента армирования для балок различной формы поперечного сечения. В данном пункте рассматриваются изгибаемые элементы из бетона класса В15 и арматуры класса А400, А500 и А600, т.е. с физической площадкой текучести и без неё.
На основании результатов расчета, построены диаграммы зависимости разрушающего момента от коэффициента армирования сечения рисунок 2.
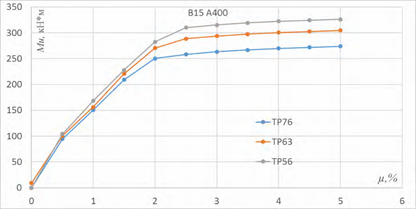
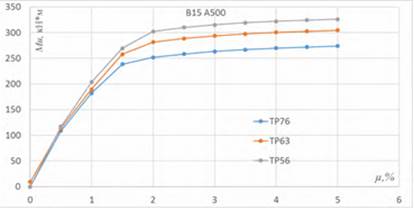
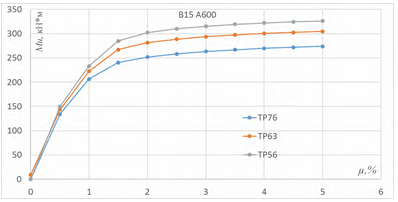
Рисунок 2. Зависимость Mu - µ для бетона В15
Как видно из рисунка 2 графики Mu – µ являются аффинноподобными. Анализ данных графиков позволяет сделать вывод, что увеличение коэффициента армирования µ для трапециевидных балок с разной формой поперечного сечения, в пределах одного класса бетона и арматуры, не сильно влияет на форму графика. Следовательно, для исследования зависимости прочности и трещиностойкости от коэффициента армирования и класса арматуры достаточно будет провести анализ трапециевидных балок одинакового поперечного сечения.
Повторим численный эксперимент для данных балок с большим числом классов бетона. В качестве исследуемых балок, принимаем железобетонные балки типа ТР76.
Для анализа влияния процентного содержания арматуры на прочность и трещиностойкость будем использовать следующие данные:
Mu- момент на стадии разрушения;
Mcrc- момент на начальной стадии трещинообразования;
Mf18- значение момента при прогибе f=18 мм (1/250 от пролета);
γrise - коэффициент прироста прочности;
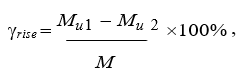 (1)
(1)
где: Mu1 - разрушающий момент при µ=x;
Mu2 - разрушающий момент при µ=x+0,5%;
γDR - коэффициент прироста момента при прогибе f=18 мм (1/250 от пролета).
По результатам исследования можно сделать следующие выводы:
- для бетона В15 увеличение коэффициента армирования выше 2% не приводит к существенному росту прочности. При m ³ 1,5% арматуру А600 следует заменить на А500, а при m ³ 2% - на А400, т.к. влияние класса арматуры на прочность железобетонных элементов трапециевидного сечения при дальнейшем увеличении коэффициента армирования µ несущественно, что хорошо видно, а;
- для изгибаемых элементов, изготовленных из бетона класса В20, наиболее оптимальный коэффициент армирования находится в диапазоне 1,0- 1,5%. Дальнейшее его увеличение выше 1,5% для арматуры классов А400, А500 приводит к несущественному приросту прочности. Разница между разрушающими моментами для балок с коэффициентом армирования µ равным 1,5 и 2%, составила 25,22% и 19,28%, соответственно, для классов А400 и А500, а для арматуры класса А600 и вовсе 9,78%;
- анализ диаграммы, представленной на рисунке Б2, в, позволяет сделать вывод о необходимости замены арматуры классов А500 и А600 арматурой А400 при m ³ 2,5% и арматуры А600 - арматурой А500 при m ³ 2%;
- для элементов, изготовленных из бетона класса В25 и арматуры класса А400, коэффициент армирования желательно принять меньше 2.5%, для арматуры классов А500 и А600 - не выше 2%, т.к. дальнейшее увеличение m не приводит к существенному росту прочности. При m ³ 2.5% использование арматуры класса А600 становится нерациональным и её следует заменить на А500, а при m ³ 3% влияние класса арматуры на деформативные и прочностные характеристики изгибаемых элементов становится незначительным, т.е. следует использовать арматуру класса А400;
- для бетона класса В40 при m ³ 3.5% арматуру класса А600 следует заменить на А500, а при m ³ 4.5% использовать только класс А400;
- для арматуры А500 прирост прочности резко падает для бетонов классов В15, В25 и В40 при коэффициентах армирования выше 1,5%, 2% и 4%, соответственно;
- при использовании арматуры А600 для балок, выполненных из бетонов классов В15-В20, В25-В30 и В40, рост прочности затухает при коэффициентах армирования выше 1,5%, 2% и 3%, соответственно;
- для арматуры классов А400 и А500 оптимальные проценты армирования из условия прочности лежат в пределах 0,5-0,7%, 1, 1,5%, 1,5-1,7 и 2-2,5% для бетонов В15, В20, В25, В30 и В40, соответственно;
- для арматуры класса А600 оптимальные проценты армирования из условия прочности лежат в пределах 0,5-0,7%, 1-1,5% и 2-2,5% для бетонов В15, В25, В40, соответственно;
- влияние класса арматуры на деформативность исследуемых образцов становится незначительным при коэффициентах армирования выше 1% для бетона класса В15, 1.5% для бетонов классов В20 и В25, 2% и 2.5%, соответственно, для бетонов классов В30 и В40;
Следует отметить, что на трещиностойкость оказывают существенное влияние только класс бетона и коэффициент армирования, а класс арматуры не оказывает почти никакого влияния.

