РЕШЕНИЕ ЗАДАЧ ПО ФИЗИКЕ ПО РАЗДЕЛУ «МЕХАНИКА»

Аннотация. В данной статье производится рассмотрение примеров основных задач, которые наиболее часто встречаются в разделе «Механика».

В Задаче 1 рассматривается пример, связанный с исследованием системы тел, в котором необходимо найти ряд кинематических и динамических величин.

В Задаче 2 рассматривается пример, связанный с исследованием системы тел с действующими между ее элементами силами тяготения. В задаче необходимо найти скорость движения одного тела относительно другого.

В Задаче 3 рассматривается движение тела по наклонной плоскости. В этой задаче необходимо найти одну силу, действующую на тело, по известным другим силам и известным соотношениям между ними.

В Задаче 4 рассматривается движение тела с изменяющейся массой. В задаче необходимо определить скорость движения тела в определённый момент времени.

В Задаче 5 рассматривается движение тела, брошенного под углом к поверхности. В задаче необходимо определить энергию, которое имеет тело в процессе движения в различных точках его траектории.

Задача 1

На однородный сплошной цилиндрический вал радиусом R=5 см и массой M = 10 кг намотана легкая нить, к концу которой прикреплен груз массой m = 1 кг.

Определите:

1) зависимость s(t), согласно которой движется груз;

2) силу натяжения нити Т;

3) зависимость φ(t), согласно которой вращается вал;

4) угловую скорость ω вала через t=1 с после начала движения;

5) тангенциальное (а_τ) и нормальное (а_n) ускорения точек, находящихся на поверхности вала в момент времени t=1c.

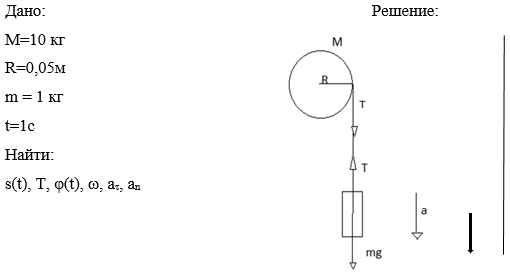
1) Система тел имеет вид, представленный на рисунке. В нем расположены цилиндрический вал, на который намотана нить, к концу которой прикреплен груз.

Запишем уравнение по 2 закону Ньютона, направив координатную ось вертикально вниз.

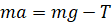
   (1)

С другой стороны, цилиндрический вал имеет момент сил вращательного движения.

Также момент сил можно представить в другом виде.

Можно записать соотношение.

          (2)

Величина  представляет собой ускорение вращательного движения.

Величина  представляет собой момент инерции вращательного движения.

Запишем соотношение c учетом формул (1) и (2) и преобразуем его.

Груз совершает равноускоренное поступательное движение при нулевой начальной скорости.

Запишем зависимость s(t) для данного груза.

Подставим в нее значение  и найдем ответ.

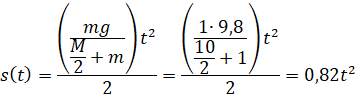
2) Силу натяжения нити определим из формул (1) и (3).

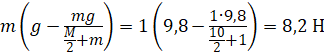
3) Вал совершает равноускоренное вращательное движение при нулевой начальной скорости.

Запишем зависимость φ(t) для вала.

Подставим в нее значение  и найдем ответ.

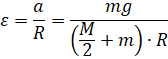
4) Запишем зависимость ω(t) для данного груза.

Подставим в нее значение  и найдем ответ при t=1 c.

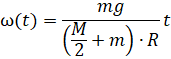
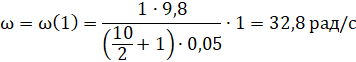
5) Определим а_τ – тангенциальную составляющую ускорения. Она равна величине a – ускорению груза.

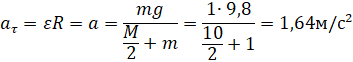
Определим а_n – нормальную составляющую ускорения при t=1c. Воспользуемся значением ω, найденным в предыдущем пункте.

Ответ: 1) ; 2) ; 3) ;

4) ; 5) ; .

Задача 2

Считая орбиту Земли круговой, определить линейную скорость движения Земли вокруг Солнца.

Орбита Земли вокруг Солнца имеет вид, представленный на рисунке.

Согласно закону всемирного тяготения.

С другой стороны, тело совершает движение по окружности, описываемое вторым законом Ньютона.

                                                                     (2)

- центростремительное ускорение можно представить как:

Объединив (1) и (2) и подставив , получим.

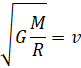
Подставляя известные значения -массы Солнца и -расстояния от Солнца до Земли и константы G, получим.

29,77км/с

Ответ: 29,77км/с

Задача 3

Вагон массой m = 1 т спускается по канатной железной дороге с уклоном α = 15° к горизонту. Принимая коэффициент трения f = 0,05, определите силу натяжения каната при торможении вагона в конце спуска, если скорость вагона перед торможением v₀ = 2,5 м/с, а время торможения t = 6 с.

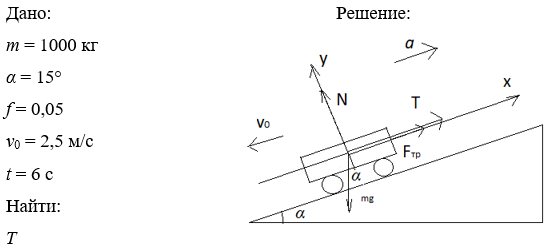
На вагон действуют силы, представленные на рисунке. Так как его движение равнозамедленное, вектор ускорения противоположен направлению его движения.

Введем систему координат так, как это представлено на рисунке, и составим систему уравнений по второму закону Ньютона.

Сила трения запишется как:

Получим.

Запишем уравнение зависимости скорости от времени.

При =6с , следовательно:

Подставив  в выражение (1) и вычислив, получим.

Ответ: 

Задача 4

Ракета с начальной массой m₀ = 1,5 кг, начинает движение из состояния покоя вертикально вверх, выбрасывая непрерывную струю газов с постоянной скоростью относительно нее скорости u = 600 м/с. Расход газа μ = 0,3 кг/c. Определить, какую скорость приобретет ракета через 1 секунду после начала движения, если она движется: 1) при отсутствии внешних сил; 2) в однородном поле силы тяжести. Оценить относительную погрешность, сделанную для данных условий задачи при пренебрежении внешним силовым полем.

1) Силы, действующие на ракету при отсутствии внешних сил, представлены на рисунке а).

Согласно формуле Циолковского:

Масса ракеты в момент времени t:

Объединяя (1) и (2) и подставляя известные значения, получим:

2) Силы, действующие на ракету при наличии внешней силы тяжести, представлены на рисунке б).

Запишем уравнение зависимости скорости от времени.

В данном случае , - собственное ускорение ракеты.

При случае, когда отсутствовали внешние силы, скорость ракеты была равна  .

Подставив все свои значения, получим:

.

3) Относительная погрешность равна:

Ответ: 1) ; 2) ; 3) .

Задача 5

Тело массой m = 0,5 кг бросают со скоростью v = 10 м/с под углом α = 30° к горизонту. Пренебрегая сопротивлением воздуха, определите кинетическую Т, потенциальную П и полную Е энергии тела: 1) через t = 0,4 с после начала движения; 2) в высшей точке траектории.

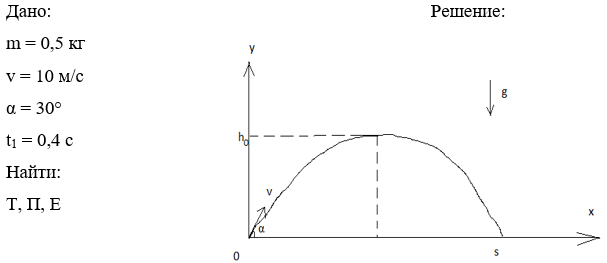
1) Траектория движения тела имеет вид, представленный на рисунке.

Согласно кинематическим уравнениям движения:

(1)

При t₁ = 0,4 с выражение (1) примет вид:

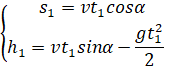
Составляющие скорости тела по осям x и y.

                          (2)

При t₁ = 0,4 с выражение (2) примет вид:

Полная скорость тела:

Кинетическая энергия тела:

Потенциальная энергия тела:

Полная энергия тела:

2) в высшей точке траектории вертикальная составляющая скорости равна нулю:

Из второго уравнения системы выразим t₀.

Приравняем к нулю величину h₀ и определим t₀:

В высшей точке траектории уравнение вертикального движения имеет вид:

Полная скорость тела:

Кинетическая энергия тела:

Потенциальная энергия тела:

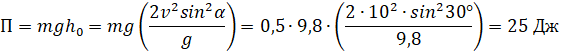
Полная энергия тела:

Ответ: 1) Е=25 Дж, Т=5,96 Дж, П=19,04 Дж 2) Е=43,75 Дж, Т=18,75 Дж, П=25 Дж.