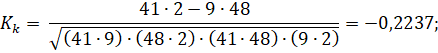ПРИМЕНЕНИЕ КОРРЕЛЯЦИОННОГО АНАЛИЗА ДЛЯ ОЦЕНКИ ВЛИЯНИЯ МЕТОДИКИ ПРОВЕДЕНИЯ СЕРТИФИКАЦИОННЫХ ИСПЫТАНИЙ ЭЛЕКТРОННОЙ КОМПОНЕНТНОЙ БАЗЫ НА КОЛИЧЕСТВО ВЫЯВЛЕННЫХ НЕСООТВЕТСТВИЙ

Электронная компонентная база (ЭКБ) составляет основу многих видов аппаратуры. Долговечность, надёжность, стабильность и корректность работы радиоэлектронной аппаратуры во многом зависят от качества электронных компонентов.

Планирование сертификационных испытаний ЭКБ предусматривает выбор методики испытаний. Для оценки влияния методики проведения сертификационных испытаний ЭКБ на количество выявленных несоответствий может быть применен корреляционный анализ. Корреляционный анализ позволяет решить две задачи:

• установить степень согласованности изменения признаков в некоторой выборке;
• доказать, что это согласованное изменение является статистически достоверным.

В простейшем варианте организации сертификационных испытаний может существовать два альтернативных качественных признака (A и B), каждый из которых принимает лишь два возможных качественных значения (a₁ и a₂, b₁ и b₂). Значения измерены с помощью номинативных шкал. Таким образом, все испытываемые изделия могут быть разделены на четыре категории, в которых реализовались разные сочетания: {a₁, b₁}; {a₁, b₂}; {a₂, b₁}; {a₂, b₂}.

Корреляция между признаками может быть количественно описана с помощью коэффициента ассоциации Юла (Q) или коэффициента контингенции Пирсона (K_k).

Коэффициент ассоциации Юла вычисляет по формуле:

Коэффициента контингенции Пирсона вычисляет по формуле:

Для проверки достоверности корреляции вычисляется статистическая значимость по формулам:

Корреляционная связь будет считаться достоверно существующей со статистической значимостью p при выполнении условия:

где Z_кр находится по таблице критических значений стандартного нормального распределения, причем значение Z_кр выбирается для аргумента p/2. Например, при значимости p ≤ 0,05 необходимо выбирать значение Z_кр(0,025) = 1,96 [1, c.28].

Из представленных выше выражений видно, что при фиксированных n_ij всегда |K_k| < |Q|, т.е. коэффициент контингенции дает более осторожную оценку интенсивности связи. Видно также, что если хотя бы одно из четырех значений n_ij окажется равным нулю, то Q = 1, что является завышенной оценкой силы связи – в этом случае необходимо пользоваться только K_k.

Используя данные, полученные при проведении сертификационных испытаний микросхем общего применения типа ADP1111, определим имеется ли связь между выбранной методикой испытаний и количеством выявленных несоответствий.

Проверяемые гипотезы:

H0: Значимая корреляционная зависимость между показателями отсутствует;

H1: Существует достоверная корреляционная зависимость между показателями.

Представим исходные данные в виде таблицы 2.

Таблица 2.

Исходные данные по результатам испытаний

Коэффициент ассоциации Юла:

Коэффициент контингенции Пирсона:

Статистическая значимость:

По таблице критических значений стандартного нормального распределения для p ≤ 0,05 находим: Z_кр(0,025) = 1,960.

Поскольку для обоих методов Z > Z_кр(0,025), принимается экспериментальная гипотеза: между выбранной методикой сертификационных испытаний ЭКБ и результатами испытаний имеется тесная корреляционная связь: сильная по коэффициенту ассоциации Юла и заметная по коэффициенту контингенции Пирсона. То, что связь не оказывается очень сильной свидетельствует о существовании каких-то неучтенных факторов.