Расчет стенок цилиндрических резервуаров на осесимметричные нагрузки

В последние десятилетия при строительстве гражданских и промышленный зданий широко применяются железобетонные тонкостенные пространственные покрытия. В них используются разнообразные по форме оболочки в сочетании с различными опорными контурными конструкциями.

Тонкостенные пространственные покрытия имеют ряд преимуществ по сравнению с покрытиями из плоскостных конструкций-ферм, арок, балок, кровельных панелей. Ими можно перекрывать большие площади, а также они имеют меньшую массу, что весьма важно при больших пролетах. В них удачнее сочетаются ограждающие и несущие функции. Богатое разнообразие геометрических форм оболочек придает особую архитектурную выразительность пространственным покрытиям. Тонкостенные пространственные покрытия применяются в первую очередь в таких зданиях, как ангары, спортивные залы, крытые рынки, выставочные павильоны, вокзалы, многие производственные здания и т.п..

В практике строительства преимущества тонкостенных пространственных конструкций, несмотря на непрерывное их совершенствование, пока еще реализуются не полностью.

Рассмотрим стенку круглого резервуара в общем случае переменной толщины, загруженную осесимметричной нагрузкой (рис. 1) [1]:

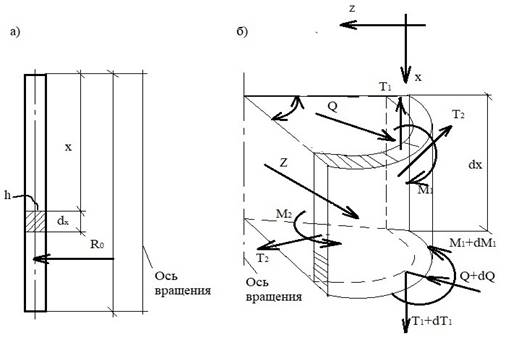
Рисунок 1. Стенка круглого резервуара

Из условий равновесия в направления оси z бесконечно малого элемента стенки (рис.1-а), вырезанного двумя меридиональными сечениями, образующими угол dᴪ (рис.1-б), и двумя параллельными кругами на расстоянии x и (x+dx), имеем:

; ,                                                                              (1)

Где:

Ro-радиус срединной поверхности оболочки;

x-расстояние, считываемое от какой-либо точки вдоль образующей;

Q-поперечная сила в сечении, перпендикулярном образующей цилиндра;

T₂-кольцевые усилия;

М₁-меридиональный изгибающий момент;

Z-нормальная к срединной поверхности оболочки компонента внешней нагрузки.

Положительное направление усилий и осей координат показано на рис.1.  Два уравнения системы (1) содержат три неизвестные величины: Т₂, Q и М₁. Следовательно, задача является статически неопределимой [2], и для ее решения необходимо рассмотреть деформации оболочки. Относительное удлинение срединной поверхности оболочки в кольцевом направлении при ее перемещении в радиальном направлении на величину ω определится по формуле:

                                                                                  (2)

Кривизна образующей срединной поверхности оболочки при небольших перемещениях ὠ приближенной представляется зависимостью:

                                                                                                 (3)

Отсюда, согласно закону Гука:

                                                                                    (4)

Где D=(Eh³)/12- изгибная жесткость оболочки (коэффициент Пауссона пренебрегая).

Исключаем из системы уравнений (1) поперечную силу Q, получим

                                                                                            (5)

Подставив в (5) зависимости (4), окончательно найдем

                                                                             (6)

Уравнение (6) является основным разрешающим уравнением симметрично-загруженной цилиндрической оболочки с толщиной стенки, изменяющейся по любому закону.

В практике резервауростроения наиболее часто приходится встречаться с цилиндрическими оболочками, имеющими постоянную толщину стенки или изменяющуюся по линейному закону.

При постоянной толщине h стенки оболочки уравнение (6) одно с уравнением изгиба балки постоянной жесткости на упругом основании, имеющем постоянный коэффициент постели. Действительно, при D=const уравнение (6) принимает вид:

                                                                                                            (7)

Для решения (7) введем новую независимую переменную, определяемую по формуле

                                                                                                                     (8)

Уравнение (7), записанное относительно новой переменной, будет иметь вид

                                                                                                          (9)

Уравнение (9) представляет собой неоднородное дифференциальное уравнение четвертого порядка с постоянными коэффициентами [3, с.113]. Как известно, общее решение неоднородного уравнения состоит из общего решения, соответствующего ему однородного уравнения

                                                                                                              (10)

И какого-нибудь одного частного решения неоднородного уравнения (9). В качестве последнего в дальнейшем будем принимать решение, соответствующее без моментному напряженному состоянию оболочки. Для осесимметричной нагрузки это решение весьма просто. Так, например, если поверхностной нагрузкой на оболочку считать гидростатическое давление Z=yx (где y-удельный вес жидкости, x- расстояние от верхнего края оболочки), то решениями, соответствующими без моментному напряженному состоянию, будут:

                                                                                                         (11)

Общее решение уравнения (10) имеет вид:

                                                                                                  (12)

Где e-основание натуральных логарифмов;

с₁,…с₄-постоянные интегрирования.

Если расстояние между краями оболочки достаточно велико, то нагрузка на одном краю оболочки не вызывает деформаций и напряжений в зоне противоположного края оболочки, а именно при l/s>2,5 высоту стенки l можно считать бесконечно длинной [1, с. 113]. В цилиндрических стенках резервуаров это условие в большинстве случаев выполняется, т.е. вместо (11) моно принять:

                                                                                                             (13)

Тогда изгибающий момент М1, поперечная сила Q, кольцевое усилие Т₂ и угол поворота будут:

                                                                                            (14)

Определив из краевых условий произвольные постоянные с₁ и с₂ и подставив их в формулы (14) и (1), получим соответственно усилия и перемещения в любой точке оболочки. Так, приняв за начало отсчета φ нижний край оболочки, загруженный изгибающий момент Мо, получим:

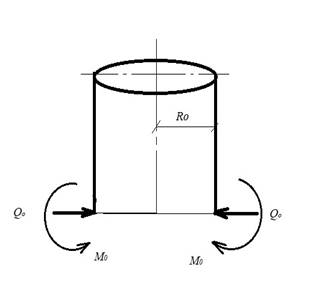
Рисунок 2. Действие изгибающих моментов

                                                                                                    (15)

Подставляя (15) в формулы (14) и (13), найдем:

                                                                                                           (16)

Значения первых двух выражений (16) при Мо=1 и φ=0 называются коэффициентами влияния краевой упругой деформации. Эти величины используются при расчете сопряжений оболочки с кольцами и другими оболочками вращения. Они имеют такой вид:

                                                                                                   (17)

При 

Определим постоянные интегрирования при загружении этого же края оболочки поперечной силой Qо, т.е.:

                                                                                                     (18)

Подставляя С_1Q и C_2Q из (18) в формулу (13) и (14), найдем в любой точке оболочки внутренние усилия и перемещения:

                                                                                                    (19)

D-кратные значения первых двух выражений (19) при Q_o=1 и φ=0 называются коэффициентами влияния краевой упругой деформации цилиндрической оболочки и обозначаются так:

                                                                                                 (20)

Итак, а₁₁-это D-кратный угол поворота края оболочки от краевого момента М_о=1 по направлению этого момента; а₁₂-это D-кратное перемещение края оболочки, вызванное краевым моментом М_о=1 по направлению Q₂. При низких стенках резервуаров, когда l/s<2.5 необходимо учитывать взаимное влияние противоположных краевых условий.

В настоящее время такие расчеты производят при строительстве резервуаров как из железобетона, так и из стали, что позволяет улучшать технологии строительства и обильно применяется для хранения горюче-смазочных материалов (рис. 3,4):

Рисунок 3. Железобетонный резервуар

Рисунок 4. Стальные резервуары для нефтепродуктов