Разработка и анализ алгоритма сортировки на основе использования бинарных деревьев

Бинарное дерево поиска – это достаточно базовая, но в то же время интересная структура данных, у которой, к тому же, существует большое количество модификаций и вариаций, а также применений на практике.

В теории графов дерево представляет собой ориентированный или неориентированный граф, не содержащий циклов. То есть для любой вершины существует один и только один способ добраться до любой другой вершины. В программировании широко используются такие динамические структуры данных, как бинарные деревья, в которых число исходящих дуг не превосходит двух, и N-арные деревья (с произвольным количеством исходящих ребер).

Введем некоторые понятия для графа-дерева, у которого вершинами являются вершины дерева, а дугами – ветви дерева. Начальная вершина, называемая корнем, изображается в верхней части дерева, и считается, что она находится на нулевом уровне. Вершина Y, располагаемая ниже вершины X и соединенная с ней ветвью, называется непосредственным потомком вершины X, или ее дочерней вершиной (а вершина X, соответственно, – непосредственным предком вершины Y, или ее родительской вершиной). Если вершина X находится на уровне I, то все ее непосредственные потомки находятся на уровне I+1. На графе, изображающем дерево, все вершины одного уровня располагаются на одной горизонтали. Номер максимального уровня дерева называется глубиной (или высотой) дерева. Если вершина не имеет потомков, то она называется листом (терминальной вершиной). Нетерминальная вершина называется внутренней. Число непосредственных потомков внутренней вершины дерева называется степенью этой вершины. Максимальная степень всех вершин дерева называется степенью дерева. Дерево называется упорядоченным, если все непосредственные потомки любой вершины упорядочены.

В памяти компьютера деревья обычно представляют в виде связной структуры, где каждый узел помимо ключа (key) хранит указатели на дочерние узлы и иногда на родительский. Для хранения двоичных (бинарных) поисковых деревьев используют структуру с левыми и правыми поддеревьями, где для каждого узла X выполняется следующее свойство:

·     если узел Y лежит в левом поддереве узла X, то key[Y] < key[X];

·     если узел Y лежит в правом поддереве узла X, то key[Y] > key[X].

Такая структура данных широко применяется в алгоритмах сортировки. Сортировка с помощью двоичного дерева — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. То есть если мы будем выполнять операцию обхода дерева по правилу «левый сын-родитель-правый сын», то, записывая все встречающиеся элементы в массив, получим упорядоченное в порядке возрастания множество.

На каждой итерации мы спускаемся на один уровень вниз, поэтому время поиска узла в двоичном дереве поиска, то есть, количество шагов, ограничено сверху высотой этого дерева. Используя О-символику, можно обозначить время поиска в худшем случае как O(h), где h – высота дерева.

Мы разработали собственный Бинарный алгоритм сортировки массивов на основе бинарных деревьев, который основан на том, что для каждой вершины, начиная с корня, используется правило «влево уходит старший сын, вправо – младший брат». Алгоритм Бинарной сортировки (по возрастанию):

Шаг 1. Преобразование к бинарному дереву: Исходную последовательность данных представляем в виде бинарного дерева таким образом, что для каждого элемента в левое поддерево уходят числа, большие либо равные предыдущему числу последовательности, а в правое – меньшие. В результате получаем структуру в виде одной ветки.

Шаг 2. Сравнение: Начиная с самого нижнего листа, мы движемся вверх до тех пор, пока не обнаружим, что следующая вершина имеет большее значение (если данное условие не выполняется, значит, последовательность отсортирована).

Шаг 3. Выделение пустой вершины: К найденной вершине, значение которой больше значения потомка, навешиваем вторую пустую вершину (значение не определено).

Шаг 4. Сдвиг: Вершина с большим значением сдвигается на пустое место (в левое поддерево), правое поддерево смещается верх на одну позицию. В результате, крайняя дочерняя вершина оказывается с пустым значением. Освободившаяся пустая вершина удаляется.

Шаг 5. Приведение к виду бинарного дерева: Представляем получившееся упорядоченное дерево в виде ветки.

Шаги повторяются до тех пор, пока номер каждой последующей вершины не будет больше номера предыдущей, т.е. пока последовательность не будет отсортирована.

На рисунке 1 представлено сравнение времени выполнения данного алгоритма сортировки с пузырьковой и древесной алгоритмами.

Рисунок 1. График зависимости времени сортировки от длины последовательности

Как известно, сложность алгоритма прямо зависит от длины последовательности. Так для простейшей сортировки пузырьком эта зависимость квадратичная O( ), где n – количество элементов сортируемого массива, что весьма неэффективно, поэтому алгоритм считается учебным и почти не применяется вне учебной литературы. Общее быстродействие метода древесной сортировки составляет O(n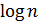), основным недостатком является требование к памяти под дерево.

Что касается созданного нами алгоритма, сложность данного алгоритма составляет O( ) в среднем случае, где шаги преобразования массива данных к бинарному дереву и обратно составляет O(n), а операции вставки и удаления элементов в среднем случае имеют сложность O( ), а в случае разбалансированного дерева O(n), что может привести к сложности всего алгоритма Бинарной сортировки порядка O( ).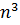

На рисунке 2 представлено сравнение времени работы алгоритма для произвольной последовательности и наиболее «неблагоприятного» случая (когда последовательность отсортирована в порядке, обратном требуемому).

Рисунок 2. График зависимости времени сортировки от степени упорядоченности элементов последовательности

Недостатком являются также большие требования к памяти. Очевидно, нужно n места под ключи и, кроме того, память на 2 указателя для каждого из них.

Таким образом, такой алгоритм нельзя отнести к группе быстрых, т.к. при большом количестве входных данных его использование не является оптимальным по времени и расходам памяти. Значит, существующий алгоритм древесной сортировки является более эффективным.