Об одной программной реализации многопоточного умножения целых чисел большой разрядности

Аннотация. В статье рассматривается программная реализация алгоритма многопоточного умножения целых чисел большой разрядности. Интерес к данной теме основан на том, что арифметика с числами большой разрядности широко используется в системах с ассиметричным шифрованием и в алгоритмах, связанных с факторизацией больших целых чисел.

Abstract. The article deals with the software implementation of the algorithm for multithread multiplication of integers of large-digit numbers. Interest in this topic is based on the fact that arithmetic with large-digit numbers is widely used in systems with asymmetric encryption and in algorithms related to the factorization of large integers.

Ключевые слова: параллельные и последовательные алгоритмы, алгоритм многопоточного умножения больших чисел.

Keywords: Parallel and sequential algorithms, algorithm for multi-thread multiplication of large numbers.

В последнее время все большее применение находят системы асимметричной криптографии, для реализации которых требуется применять целочисленные вычисления с числами большой разрядности, и исследуются различные быстрые алгоритмыумножения таких чисел [1].

В данной публикации рассматривается программный модуль, в котором реализуется алгоритм многопоточного умножения целых чисел большой разрядности – далее ЦБР-чисел (под числом большойразрядности будем понимать число, состоящееиз нескольких тысяч или миллионов двоичных знаков). В качестве языка реализации выбран компилятор FreePascal IDE for Win32 for i386 (Compiler Version 2.6.4), а в качестве операционной системы – Windows XP.

В качестве объектов исследования рассматриваются классический алгоритм умножения «столбиком» и алгоритм многопоточного умножения ЦБР-чисел.

Прежде чем переходить к детализации алгоритма многопоточного умножения, поясним его основную идею на примере умножения двух чисел 79478310 и 972110.

Результатом умножения будет число 772608554310, которое получается в результате следующих действий – выполнения промежуточных умножений и арифметических сдвигов с последующим результирующим суммированием (в соответствии с рисунком 1)

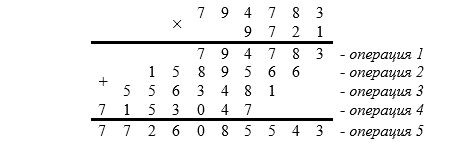
Рисунок 1. Результат умножения двух целых чисел классическим способом

В то же время последовательность указанных действий можно выполнить и в произвольном порядке (в соответствии с рисунком 2):

Рисунок 2. Модифицированный алгоритм умножения двух целых чисел

Из рисунка 2 видно, что выполнение последовательности действий «операция i» (i=1..4)может осуществляться в произвольном порядке с последующим результирующим суммированием «операция 5». Именно на этом свойстве суммирования и будет основан алгоритм многопоточного умножения, когда «операция i» (i=1..4) выполняется в отдельном потоке с последующим результирующим суммированием.

Опишем более детально основные моменты алгоритма многопоточного умножения. Пусть заданы два ЦБР-числа А и В, где число А имеет длину в m+1 цифр в системе счисления по основанию BASE (BASE>1), которое можно представить следующим образом:

А = a_ma_m-1…a₀ ,

где: a_i– значенияиз диапазона 0 .. BASE-1.

В соответствии с определением числа, представимого в позиционной системе счисления по основания BASE, число А можно представить следующим образом:

 А = a₀ + a₁´ BASE + … + a_m-1´ BASE ^m-1 +a_m´ BASE ^m                                                        (1)

В формуле (1) произведем группировку слагаемых таким образом, чтобы число А было представимо в системе счисления по основанию BASE^P, где p = (m+1) div k - количество элементов в группе,(k+1) - количество групп. Тогда получим:

А=,                                           (2)

где: div, mod–операции получение частного и остатка при целочисленном делении.

Тогда из формулы (2) при умножении числа А на число В получаем:

А´В =                                      (3)

Из формулы (3) следует, что умножение числа А на число В сводится к умножению числа В на более «короткие части» числа А и максимум k+1 сложений полученных результатов умножений. Процедуру умножения числа В на более «короткие части» числа А можно будет реализовать в отдельных процессах/потоках. Таким образом, при наличии в вычислительной системе более одного процессора (или при наличии нескольких ядер процессора) следует ожидать сокращения времени выполнения операцииумножения для ЦБР-чисел.

Продемонстрируем работу алгоритма потокового умножения чисел А и В (результат будет храниться в переменной R) с помощью рисунков 3–5.

Этап 1: Формирование контекста окружения потоков.

Например, пусть для чисел A и В значения А.MSB и В.MSB равны соответственно3381 и 300 (при А.LSB=В.LSB=0), элементы массива данных, соответствующие числам А и В (A.BigNumber и В.BigNumber) заполнены произвольными числовыми значениями, число потоков равно 17, а элементы массива ContextList (массив данных контекста окружения потоков), будут представлены следующими значениями (таблица 3):

Таблица 3.

Формирование значений контекста окружения потока, этап 1

^* – значения присваиваются службами ОС Windows и отличаются от указанных значений;

^** – на момент начала работы алгоритма умножения массив Res заполнен нулевыми значениями;

^*** – ссылки на ЦБР-числа А и В соответственно

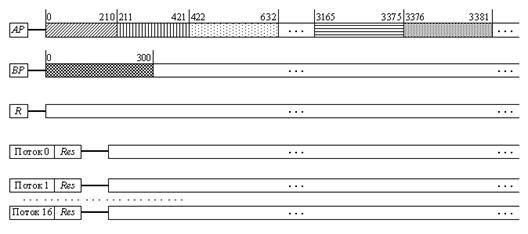
Рисунок 3. Формирование блоков данных для числа АP

Комментарии к рисунку 3:

·     области, заштрихованные различными видами узоров, представляют собой элементы блоков данных с произвольными числовыми значениями;

·     не заштрихованные области – элементы массива, содержащие нулевые значения;

·     числовые метки над заштрихованными областями – это числовые значенияначалаиконца соответствующих блоков ЦБР-чисел А и В.

После формирования данных контекста окружения, начинает выполняться этап 2 – этап выполнения умноженияблоков значений из массива числа А на число В. Содержание этого этапа можно представить в соответствии с рисунками 4 и 5 (на примере умножения в двух потоках):

Этап 2: Умножение в потоках.

Рисунок 4. Выполнение умножения блока данных числа А на число В потоке с номером 0

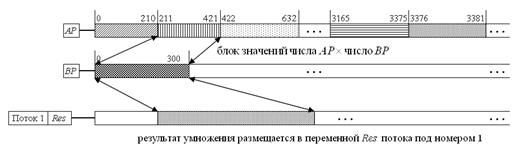
Рисунок 5. Выполнение умножения блока данных числа А на число В потоке с номером 1

Анализ действий алгоритма на представленных рисунках 4 и 5 показывает, что вычисления производятся независимо друг от друга и результаты промежуточныхвычислений не искажают друг друга. После окончания этапа 2 наступает этап 3 – этап результирующего суммирования.

Этап 3. Этап результирующего суммирования.

Содержание этапа 3 заключается в том, что все промежуточные вычисленные значения (которые хранятся в контексте окружения каждого потока в массиве Res), суммируются в итоговом ЦБР-числе R. Результирующее суммирование выполняется с каждым из полученных блоков данных Res и соответствующим блоком данных числа R (в соответствии с рисунком 6).

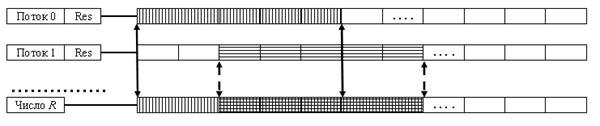
Рисунок 6. Выполнение этапа 3 – этапа результирующего суммирования

Следует отметить, что результирующее суммирование выполняется сразу же по окончании вычислений тем или иным потоком.

Результаты:

По результатам тестирования были получены следующие результаты:

·     время выполнения алгоритма последовательного умножения в два раза превышает время выполнения многопоточного умножения для многоядерных (однопроцессорных) систем (коэффициент ускорения вычислений k=2);

·     коэффициент k на тестируемых компьютерах не изменялся при увеличении количества ядер процессора (тестировались однопроцессорные системы с двумяи четырьмя ядрами);

·     на тестируемых компьютерах для ЦБР-чисел<500 байт классическое умножение эффективнее многопоточного умножения;

·     при значительном увеличении числа потоков (>64) наблюдалось уменьшение коэффициента k (большое количество потоков начинает скорее «угнетать» операционную систему, чем способствовать ускорению вычислений).

Выводы:

Анализируя полученные результаты можно сделать следующие выводы:

·     алгоритм многопоточного умножения является масштабируемым;

·     алгоритм многопоточного умножения может быть реализован как в OPENMP, так и в MPI-подобных системах;

·     использование механизмов распараллеливания вычислительных процессов позволяет сократить общее время выполнения вычислений;

·     можно предположить, что использование систем с несколькими процессорами и общей памятью позволит повысить коэффициент k пропорционально количеству процессоров;

·     алгоритм умножения в потоке может быть заменен на любой алгоритм быстрого умножения.

По результатам разработки модуля следует сделать следующие замечания:

·     модуль в основном тестировался в инструментальной среде программированияFreePascal IDE for Win32 for i386 в режиме Delphi Compatible;

·     данную схему вычислений следует рассматривать как некую одностороннюю схему, в которой только одно ЦБР-число разбивалось на блоки. Анализ алгоритма показывает, что данную схему можно реализовать и как двустороннюю, когда оба ЦБР-числа разбиваются на блоки, которые будут умножаться в отдельных потоках;

·     демонстрируемое ускорение в вычислениях (в 2 раза) достигается за счет экстенсивных методов, то есть за счет использования механизмов параллелизма операционной системы и за счет более интенсивного использования вычислительных ресурсов процессора;

·     ускорение вычислений при многопоточной реализации может быть достигнуто только для систем, имеющих как минимум несколько ядер в процессоре.