КИНЕТИЧЕСКИЕ ПАРАМЕТРЫ РОСТА ШТАММОВ ESCHERICHIA COLI ПРИ ВОЗДЕЙСТВИИ МИНИМАЛЬНО ИНГИБИРУЮЩЕЙ КОНЦЕНТРАЦИИ (МИК) АМОКСИКЛАВА

KINETIC GROWTH PARAMETERS OF Escherichia coli STRAINS EXPOSED TO THE MINIMUM INHIBITORY CONCENTRATION (MIC) OF AMOXICLAV

Anna Timoshenko

Master’s student, NAO Karaganda Medical Universiry, Republic of Kazakhstan, Karaganda

Аннотация. Статья посвящена сравнению кинетических параметров роста штаммов Escherichia coli с разной чувствительностью к амоксиклаву при культивировании в среде с минимальной ингибирующей концентрацией антибиотика. Применение методов микробиологии, спектрофотометрии, а также математического моделирования на Python позволило выявить различия в кинетических параметрах (предельная ёмкость, скорость роста, начальная численность) штаммов. Устойчивый штамм показал наибольшую предельную ёмкость, промежуточно-устойчивый — максимальную скорость роста.

Abstract. The article focuses on comparing the kinetic growth parameters of Escherichia coli strains with varying sensitivity to amoxiclav during cultivation in a medium containing the minimum inhibitory concentration of the antibiotic. The use of microbiological methods, spectrophotometry, and mathematical modeling in Python made it possible to identify differences in kinetic parameters (carrying capacity, growth rate, initial population size) among the strains. The resistant strain exhibited the highest carrying capacity, while the intermediate-resistant strain showed the highest growth rate. These findings are important for the development of effective antibiotic therapy.

Ключевые слова: Escherichia coli; амоксиклав; чувствительность к антибиотику; математическое моделирование.

Keywords: Escherichia coli; amoxiclav; antibiotic sensitivity; mathematical modeling.

Escherichia coli, помимо своей роли ключевого элемента нормальной кишечной микрофлоры, выступает возбудителем как госпитальных, так и внебольничных инфекций у человека. Подобно другим бактериальным патогенам, E. coli способна развивать резистентность, включая множественную устойчивость к различным классам антимикробных средств, что существенно затрудняет терапию инвазивных инфекций, вызванных этим микроорганизмом. Комбинация амоксициллина и клавулановой кислоты (AMC) относится к числу широко применяемых антимикробных препаратов в ряде стран, преимущественно для лечения инфекций дыхательной и мочевыделительной систем. Тем не менее, данные о её влиянии на развитие антибиотикорезистентности, особенно у E. coli, остаются ограниченными [1,С 2214-2218]. МИК (минимальная ингибирующая концентрация) служит ключевым параметром для выбора эффективной терапии. В моделировании роста бактерий МИК позволяет количественно оценить ингибирующее действие антибиотика [2, С 107].

Цель исследования. Провести сравнительный анализ кинетических параметров роста штаммов Escherichia coli с различной чувствительностью к амоксиклаву при культивировании в среде, содержащей минимальную ингибирующую концентрацию (МИК) данного антибиотика.

Материалы и методы. Были использованы микробиологические методы (метод суточного культивирования микроорганизмов, подготовка микробной взвеси, метод серийных разведений, определение МИК). Первым этапом мы получали суточные культуры штаммов E.Coli (устойчивого, промежуточно-устойчивого, чувствительного). Для этого стерильным шпателем берется небольшое количество микробной культуры и делается рассев на питательные среды методом Дригальского. Инкубация проходит в термостате в течение 18-24 часов. На следующий день из выращенных культур делается взвесь 0,5 стандарт мутности по Макфарланду в 2 мл физраствора  и разливается в 96-луночные планшеты в объеме 100 мкл,  куда впоследствии будет добавлен амоксиклав методом серийных разведений (взвесь антибиотика включает в себя 0,064 гр порошка амоксиклава, 1 мл физраствора, 4 мл Мюллер-Хинтона бульона). Инкубация занимает 18-24 часа. По степени мутности в лунках планшета определяется МИК (минимальная ингибирующая концентрация) антибиотика для каждого штамма [3, С 163-175].

Спектрофотометрический метод анализа проводился на автоматическом ИФА- анализаторе Tecan freedom evolyzer 200 с целью определения оптической плотности каждого исследуемого штамма каждые 60 минут в течение 21 часа измерений при воздействии МИК. Инкубация проводилась в Shaker-Thermostat Sky Line. Полученные данные в виде таблицы были оформлены в Excel. Метод математического моделирования проведен в мультипарадигменном языке программирования Python, с использованием логистической модели были определены кинетические параметры роста исследуемых штаммов [4].

Результаты исследования. В проведенном исследовании сравнивали кинетические параметры роста трех штаммов Escherichia coli: устойчивого, промежуточно-устойчивого и чувствительного к амоксиклаву. Кинетические показатели роста (K– предельная ёмкость среды, r-скорость роста популяции, N0–начальная численность популяции.) были рассчитаны на основе логистических моделей роста исследуемых штаммов. Логистическая модель роста описывается дифференциальным уравнением, которое в 1838 году предложил Пьер-Франсуа Ферхюльст [5, С 1875-1881].

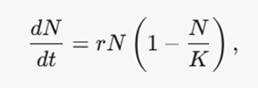
Рисунок 1. Дифференциальное уравнение Пьера-Франсуа Ферхюльст

где:

• N — численность популяции (например, плотность бактериальных клеток, измеряемая как оптическая плотность).
• t — время.
• r — удельная скорость роста (коэффициент, характеризующий скорость размножения в оптимальных условиях).
• K — емкость среды (максимальная численность популяции, которую может поддерживать среда, ограниченная ресурсами или стрессовыми факторами, такими как антибиотик).
• dN/dt​ — скорость изменения численности популяции.

Измерение оптической плотности (OD) с течением времени позволило построить кривые роста и подогнать их к логистической модели для определения r и K для каждого штамма. Оценку точности моделей проводили на основе MAPE и R², так же обращали внимание на распределение остатков. Надежность созданных моделей роста оценивали при помощи кросс-валидации.

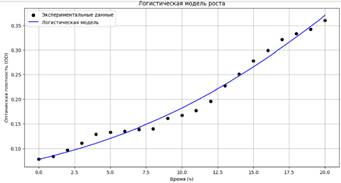
Рисунок 2. Логистическая модель роста устойчивого штамма

Оптимальные параметры логистической модели роста устойчивого штамма:

K = 1.000, r = 0.097, N0 = 0.078, MAPE: 5.28%; R²: 0.984

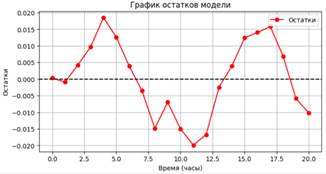
Рисунок 3.  График остатков логистической модели роста устойчивого штамма

Статистика Шапиро-Уилка: 0.962, p-значение: 0.563977. Остатки близки к нормальному распределению.

Значение MAPE (5.28%) указывает на низкую среднюю процентную ошибку прогнозов, что свидетельствует о хорошем соответствии модели данным. Высокий коэффициент детерминации R² (0.984) подтверждает, что модель объясняет 98.44% вариации данных, демонстрируя сильную корреляцию между предсказанными и наблюдаемыми значениями. Статистика Шапиро-Уилка (p-значение 0.563) и близость остатков к нормальному распределению указывают на отсутствие значительных отклонений от нормальности, что дополнительно подтверждает адекватность модели.

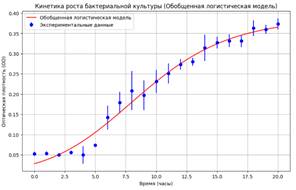
Рисунок 4.  Обобщенная логистическая модель роста устойчивого штамма (кросс-валидация)

Метрики точности: R²: 0.9808; MAPE: 12.84%

Модель демонстрирует выcокую точность (высокий R²), эффективно описывая влияние амоксиклава в минимальной ингибирующей концентрации на рост кишечной палочки. Использование МИК подчеркивает способность модели улавливать тонкие изменения в росте бактерий на границе ингибирования. MAPE на уровне 12.84% свидетельствует о высокой точности, но оставляет пространство для оптимизации, например, за счет добавления новых признаков или настройки гиперпараметров, чтобы минимизировать процентную ошибку.

Рисунок 5. Логистическая модель роста промежуточно-устойчивого штамма

Оптимальные параметры: K = 0.320, r = 0.255, N0 = 0.034.

MAPE: 13.32%; R²: 0.961

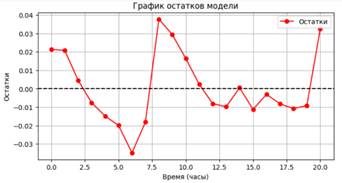
Рисунок 5. График остатков логистической модели роста промежуточно- устойчивого штамма

Статистика Шапиро-Уилка: 0.937, p-значение: 0.190. Остатки близки к нормальному распределению.

Значение MAPE (13.32%) указывает на умеренную среднюю процентную ошибку, что говорит о хорошей предсказательной способности модели. Коэффициент детерминации R² (0.961) показывает, что модель объясняет 96.06% вариации данных, что свидетельствует о сильной корреляции между предсказанными и наблюдаемыми значениями. Статистика Шапиро-Уилка (p-значение 0.190) говорит о близости остатков к нормальному распределению, что поддерживает адекватность модели.

Рисунок 6.  Обобщенная логистическая модель роста промежуточно- устойчивого штамма (кросс-валидация)

Метрики точности: R²: 0.9466; MAPE: 15.76%

Модель демонстрирует высокую точность (высокий R²), эффективно описывая влияние амоксиклава в минимальной ингибирующей концентрации на рост кишечной палочки. Использование МИК подчеркивает способность модели улавливать тонкие изменения в росте бактерий на границе ингибирования. Тем не менее, MAPE на уровне 15.76% является допустимой нормой в биологических исследованиях, однако требует дальнейшего анализа с целью улучшения модели за счет оптимизации гиперпараметров.

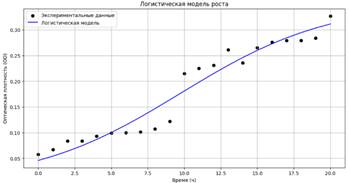
Рисунок 7. Логистическая модель роста чувствительного штамма

Оптимальные параметры полученной модели: K = 0.354, r = 0.195, N0 = 0.046. MAPE: 12.91%; R²: 0.944.

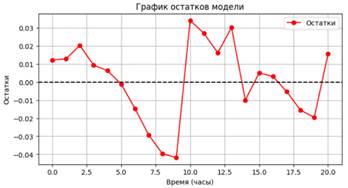
Рисунок 8.  График остатков логистической модели роста чувствительного штамма

Статистика Шапиро-Уилка: 0.961, p-значение: 0.528. Остатки близки к нормальному распределению.

Значение MAPE (12.91%) указывает на умеренную среднюю процентную ошибку, что отражает удовлетворительную предсказательную способность модели. Коэффициент детерминации R² (0.943) показывает, что модель объясняет 94.36% вариации данных, свидетельствуя о сильной корреляции между предсказанными и наблюдаемыми значениями. Статистика Шапиро-Уилка (p-значение 0.528) и близость остатков к нормальному распределению подтверждают отсутствие значительных отклонений от нормальности, что указывает на адекватность модели.

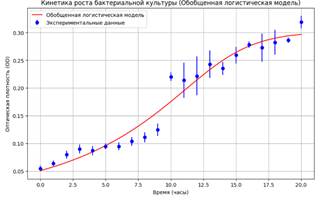
Рисунок 9.  Обобщенная логистическая модель роста чувствительного штамма (кросс-валидация)

Метрики точности: R²: 0.9602; MAPE: 9.66%

Модель демонстрирует высокую точность (высокий R²), эффективно описывая влияние амоксиклава в минимальной ингибирующей концентрации на рост кишечной палочки. Использование МИК подчеркивает способность модели улавливать тонкие изменения в росте бактерий на границе ингибирования. MAPE на уровне 9.66% свидетельствует о превосходной точности предсказаний, хотя дальнейшая оптимизация может еще больше улучшить результаты.

Проведенные исследования показали, что наибольшая предельная скорость среды (максимально возможная численность популяции) наблюдалась у устойчивого штамма K = 1.000, далее идет чувствительный K = 0.354, самый низкий показатель K = 0.320 у промежуточно-устойчивого штамма. Наибольшая скорость роста популяции r = 0.255 была выявлена у промежуточно-устойчивого штамма, далее r = 0.195 у чувствительного штамма, и r = 0.097 у устойчивого штамма. Начальная численность популяции N0 = 0.078 была выявлена у устойчивого штамма, далее N0 = 0.046 - у чувствительного штамма, и наименьшее значение N0 = 0.034 у промежуточно- устойчивого штамма.

Построенные логистические модели роста успешно описывали поведение штаммов, что подтверждалось значениями метрик точности (MAPE и R²) и кросс-валидации.

Выводы. Выявленные различия в кинетических параметрах подчеркивают необходимость учета специфики каждого штамма при интерпретации данных. Различия в кинетических параметрах могут быть связаны с генетическими или физиологическими особенностями штаммов, влияющими на их устойчивость к амоксиклаву. Например, устойчивый штамм обладает механизмами активного выведения антибиотика или его инактивации. Низкая предельная ёмкость промежуточно-устойчивого штамма при высокой скорости роста требует дополнительного изучения. Возможно, это связано с накоплением токсичных метаболитов или истощением ресурсов среды на поздних стадиях. Полученные данные могут быть полезны для разработки стратегий применения антибиотиков, учитывающих динамику роста бактерий с различной чувствительностью.