Алгоритм решения задачи квадратичного выпуклого программирования методом последовательного перебора граней

ALGORITHM OF DECISION OF TASK OF QUADRATIC PROTUBERANT PROGRAMMING BY METHOD OF LINEAR SEARCH OF VERGES

Sergey Tatarenko

candidate of engineering sciences, associate professor, Tambov state technical university, Russia, Tambov

Аннотация. Суть предлагаемого метода решения состоит в последовательном переборе граней многогранника ограничений размерности от 0 до n-1 и поиске на этих гранях квазистационарных точек. Поиск начинается с ближайшей, видимой из точки безусловного максимума квадратичной функции, вершины.

Abstract. The essence of the proposed method lies in the sequential sorting of faces of the polyhedron of the constraints of dimension from 0 to n-1 and the faces of the quasi-stationary points. The search begins with the nearest visible point of absolute maximum of a quadratic function, the vertex.

Ключевые слова: математическое программирование; оптимизация; нелинейное программирование; квадратичная задача; квазистационарная точка.

Keywords: mathematical programming; optimization; nonlinear programming; quadratic problem; quasi-stationary point.

Задача выпуклого квадратичного программирования заключается в поиске экстремума квадратичной функции на выпуклом множестве m линейных ограничений от n переменных. Для решения такой задачи применяются различные методы, основанные на теореме Куна-Такера [1,2]. Но такие методы  требуют введения дополнительных переменных и учета нелинейных условий дополнительной нежесткости, что усложняет задачу и увеличивает ее размерность. Описанные в [3] методы перебора граней требуют последовательного решения систем линейных уравнений, порядок которых достигает 2n. В данной работе предложен точный метод решения выпуклой квадратичной задачи с ограничениями неравенствами, основанный на последовательном решении систем линейных уравнений порядка n.

Рассмотрим задачу максимизации квадратичной функции Z(x) с положительно определенной квадрикой D на замкнутом выпуклом множестве Ω линейных ограничений (неравенств)

.

В [4] показано, что с помощью поворота и масштабирования системы координат, задаваемых матрицей преобразований W, такую задачу можно свести к задаче поиска точки множества Ω, ближайшей к точке y^* безусловного максимума целевой функции, если

 ;

;   ;       ;  .

Суть предлагаемого метода решения состоит в последовательном переборе граней размерности от 0 до n-1 и поиске на этих гранях квазистационарных точек. Квазистационарная точка на грани размерности k>0 определяется с помощью проекции отрезка, соединяющего точку y^* с квазистационарной точкой на грани размерности k-1, на нормаль к грани размерности k-1, принадлежащую грани размерности k.

В общем случае грань многоугольника образована некоторым набором ограничений из m ограничений задачи, при условии обращения их в равенства, и сохранении всех остальных ограничений

.

Грань размерности 0 состоит из единственной (квазистационарной) точки, называемой вершиной, она образована пересечением n или более ограничений.

.

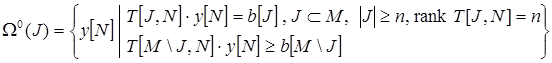Грань размерности k>0 всегда содержит в себе некоторые грани размерности k-1 и все включенные в них грани меньшей размерности. В частности, любая грань размерности 1 всегда содержит две вершины, а любая грань размерности k>1 всегда содержит не менее k+1 вершин. Грань Ω(J₁) размерности k является для грани Ω(J₂) размерности k+1 прилежащей, а грань Ω(J₂) для грани Ω(J₁) граничной, если индексное множество J₂ является подмножеством J₁

 .

Если два или более разных индексных множеств описываю одну и ту же грань, то такая грань является вырожденной

.

Невырожденная грань размерности k описывается единственным индексным множеством. Многогранник, у которого все грани невырожденные, называется простым. У невырожденной грани размерности k имеется всегда n-k прилежащих граней. Мощность индексного множества J связано с размерностью невырожденной грани, при |J|=k размерность грани равна n-k.

Количество прилежащих граней у вырожденной грани определяется мощностью множества, являющихся объединением всех индексных множеств описывающих грань

.

Все множество Ω является гранью размерности n, оно включает в себя все грани меньшей размерности, образующие границу Ω, а также внутренность  Ω .

Если точка безусловного минимума y^* = c/2 находится внутри  или на границе Ω , то есть , то она является решением задачи, в противном случае решение задачи находится на границе Ω и его можно найти последовательным перебором граней.

Перебор граней начинается с вершины, ближайшей к точке y^*, и заканчивается, если  квазистационарных точек на всех прилежащих гранях не обнаруживается. Проверяются только грани, видимые из точки y^*, т.е. в  индексном множестве которых имеется хотя бы одно из ограничений, нарушенных для точки y^*

.

Поиск начинается с нахождения видимых вершин, как решений всех возможных комбинаций систем n уравнений из m ограничений задачи

 .

Из всех вершин выберем ближайшую к y^* и назовем ее v₀ , а ее индексное множество обозначим J₀ . Если разные комбинации n уравнений из m ограничений дают одинаковые решения, то они определяют одну вершину, поэтому все индексные множества этих решений следует объединить в одно.

Определим все прилегающие к вершине v₀ грани размерности 1 (ребра) как пары вершин, одна из которых v₀, а вторая v_~0 имеет с v₀  n-1 общих активных ограничений

.

Для каждого ребра определим расстояние от него до y^* с помощью треугольника из вершин v₀ и v_~0, принадлежащих ребру, и точки y^*(рис.1).

Рисунок 1. Поиск квазистационарной точки ребра

Расстояние до ребра определяется как высота этого треугольника, опущенная из вершины y^* на основание v₀v_~0 . Поскольку точка v₀ ближайшая к y^*, то квазистационарная точка ребра v₁ ближе к точке v₀ чем к v_~0.

Определим параметры треугольника y^*v₀v_~0 :

высота –;

площадь –;

полупериметр –;

угол – .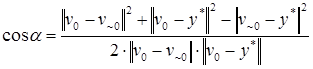

Если 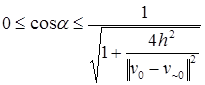, то на анализируемом ребре есть квазистационарная точка v₁, ее координаты 

.

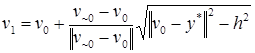При этом если   cosα = 0,   то квазистационарная точка ребра v₁ совпадает с вершиной  v₀ и эта вершина является решением задачи.

Если , то точки  v₀ и v_~0 равноудалены и квазистационарная точка находится на середине ребра  .

Затем из всех ребер, прилегающих к вершине v₀ , выберем ближайшее к точке y^*, его индексное множество обозначим J₁ и проверим все грани размерности 2,  прилежащие к выбранному ребру, т.е. имеющих с этим ребром  n-2 общих активных ограничений.  На каждой такой грани найдем квазистационарную точку. Для этого из точки v₁ построим перпендикуляр к прямой  v₀v_~0, лежащий на исследуемой грани, и найдем на нем произвольную точку v_~1.  Система уравнений для точки v_~1 будет содержать условие ортогональности прямых v₀v_~0 и v₁v_~1, а также n-2 условий активности ограничений для точки v_~1. Одну из координат точки v_~1 следует задать произвольно.

На отрезке v₁v_~1   построим треугольник, соединив концы отрезка с точкой y^* (рис.2). Высота этого треугольника будет расстоянием от аффинной оболочки исследуемой грани до точки y^* .

Рисунок 2. Поиск квазистационарной точки грани размерности 2.

Параметры треугольника y^*v₁v_~1 – высота h, площадь S, полупериметр P и угол cosα – определяются аналогично параметрам треугольника y^*v₀v_~0 .

Если cosα ≠ 0, то ближайшей точкой аффинной оболочки грани является точка

.

Для того чтобы v₂ была квазистационарной должны выполнится условия

.

Если cosα = 0 , то точка v₂ является квазистационарной и совпадает с точкой v₁.

Далее из всех граней размерности 2 выберем грань, квазистационарная точка которой ближе всех к точке y^* и исследуем все прилежащие к ней грани размерности 3. Затем исследуются грани размерности 4 и так далее до граней размерности n-1.

Процесс поиска может закончиться, если на всех прилежащих гранях не найдется квазистационарных точек. В этом случае решением задачи будет ближайшая к y^* из ранее найденных квазистационарных точек.

В общем случае исследование грани размерности k>1, с индексным множеством J_k начинается с построения нормали v_kv_~k к граничной грани меньшей размерности, лежащей на исследуемой грани. Система уравнений для нахождения точки v_~k  содержит k-1 условий ортогональности нормали к k-1 пересекающимся в точке v_~k  прямым и n-k-1 условий активности ограничений в точке  v_~k  

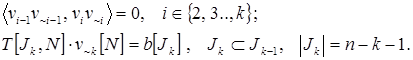
Одну из координат  v_~k следует задать произвольно.

Дополнительная точка v_~k вместе с точками v_k и y^* образует треугольник, высота которого, опущенная на сторону из точки y^* , является расстоянием до аффинной оболочки   исследуемой грани. Точка v_k+1 встречи высоты с основанием треугольника, либо c её продолжением, является квазистационарой точкой, если она удовлетворяет условиям

.

Сходимость последовательности квазистационарных точек v₀,v₁,..,v_n-1 к решению задачи обеспечивается тем, что высота каждого последующего треугольника является катетом, а высота предыдущего гипотенузой (рис.3),

Рис.3. Поиск квазистационарной точки на грани размерности 3

т.е. расстояние до каждой следующей квазистационарной точки ближе к y^*, чем  до предыдущей

.

Рисунок 3 является проекцией из 4-мерного пространства на двумерную плоскость, поэтому прямые  v₀v₃,  v₁v₃,  v₂,v₃  перпендикулярны  v₃ y^*  , а точки v₀, v₁,  v₂, v₃ не принадлежат одной плоскости (грани размерности 2).

Для получения решения задачи в исходных координатах к найденному решению  v_i следует применить обратное преобразование

.

Обозначения

N – множество целых чисел ;

|N| – мощность множества N;

– норма  вектора x ;

 – вектор с компонентами ;

 – матрица с компонентами ;

 – скалярное произведение векторов x и y ;

Список литературы:

1. Даугавет В.А. Численные методы квадратичного программирования. – СПб: Изд-во СПбГУ, 2004.– 127 с.

2. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Физматлит, 2011. – 384 с.

3. Малозёмов В.Н., Чернэуцану Е.К. О методе перебора граней в квадратичном программировании // Семинар «DHA & CAGD». Избранные доклады.10 сентября 2011 г.( http://www.dha.spb.ru/).

4. Татаренко С.И.  Линейное решение задачи квадратичного программирования // Программные продукты и системы.– 2014.– №3. – С. 36-40.