Разработка математической модели механизма для управления пространственным положением объектов с использованием аппаратно-программного комплекса на базе 8-разрядного микроконтроллера

Development of a mathematical model of the mechanism for managing the spatial position of objects using hardware and software based on 8-bit microcontroller

Evgeny Tsaregorodtsev

candidate of technical Sciences, associate Professor, The youth innovation creativity centre, Russia, Smolensk

Nikita Prokopenkov

Student, The youth innovation creativity centre, Russia, Smolensk

Alexander Rudyuk

Student, The youth innovation creativity centre, Russia, Smolensk

Egor Balaganskiy 

student of branch of the “national research UNIVERSITY “MEI”, Russia, Smolensk

Аннотация. В статье рассматривается математическая модель робота-манипулятора для исследования оптимальных режимов работы лабораторного макета. На основе теории автоматического управления средствами прикладных математических программ Scilab, приложения Xcos, получена структурная схема одноканального электромеханического объекта и проведен её анализ.

Abstract. The article deals with the mathematical model of the robot-manipulator for the study of optimal modes of laboratory layout. Based on control theory tools applied mathematical software Scilab, Xcos application, the resulting block diagram single-channel Electromechanical object and conducted its analysis.

Ключевые слова: робот, манипулятор, электромеханическая система, электропривод, кинематическое звено, манипулятор.

Keywords: robot, manipulator, Electromechanical system, electric drive, kinematic link, manipulator.

На современном этапе развития науки и техники, робототехника представляет собой неотъемлемую часть производственной деятельности человека в различных направлениях.

Понятие “робот” в настоящее время приобретает более широкий смысл, по сравнению с ранее известными определениями этого термина. Известно, что техническое устройство функционирует, как правило, в условиях некоторой неопределённости, что требует принятия решений в сложной ситуации. Возникает задача разработки математической модели исследуемого робота и прогонки её для выбора наиболее оптимальных режимов работы, а также уточнение параметров работы при критических (экстремальных) режимах.

Интерес вызывает манипуляционный робот. Он представляет собой техническое устройство с манипулятором, для совершения механических манипуляций в определённом пространстве по командам управления оператора, или по программе специального вычислителя. Рассмотрим одноканальную электромеханическую систему, функциональная схема которой изображена на рисунке 1. В ее составе – одно вращательное звено и одноканальный электропривод. Вращательные моменты на валах двигателя и редуктора  - , . Приведенный момент сопротивления - . Выходом объекта управления является угловое перемещение звена - .

Рисунок 1. Одноканальная электромеханическая система

Электропривод предназначен для преобразования маломощных электрических сигналов от устройства управления в механические воздействия (силы и моменты), мощность которых позволяет управлять нагрузкой или кинематическим механизмом. Для построения математической модели одноканального электромеханического объекта (системы), возможно использование уравнений физики, описывающих соответствующие функциональные элементы.

Кинематический механизм можно описать уравнениями на основании второго закона Ньютона:

,

,

где - угловая скорость вращения вала кинематического механизма; - вращательный момент на валу редуктора; - приведенный момент сопротивления; - приведенный момент инерции.

Модель электродвигателя представлена уравнением для момента на его валу (моментной характеристикой):

,

где - механическая постоянная; - ток якоря.

При этом напряжение, приложенное к якорю электродвигателя, имеет вид:

,

где - противо-ЭДС, - индуктивность якорной цепи; - сопротивление обмотки.

Это уравнение характеризует якорную цепь двигателя.

Аналогом его может быть:

,

где - постоянная времени;       - коэффициент передачи якорной цепи;      - противо-ЭДС.

При этом - электрическая постоянная.

Таким образом, уравнение характеризует апериодическое звено двигателя.

В соответствии с рисунком 1 усилитель мощности описывается уравнением:

,

 где   - постоянная времени усилителя мощности;

         - коэффициент усиления.

Кинематический механизм можно описать уравнением на основании второго закона Ньютона:

,

,

где - угловая скорость вращения вала кинематического механизма; - вращательный момент на валу редуктора; - приведенный момент сопротивления; - приведенный момент инерции.

Модель электродвигателя представлена уравнением для момента на его валу (моментной характеристикой):

,

где - механическая постоянная; - ток якоря.

При этом напряжение, приложенное к якорю электродвигателя, имеет вид:

,

где - противо-ЭДС, - индуктивность якорной цепи, - сопротивление обмотки.

С учётом уравнений (1)…(4) структурная схема одноканального электромеханического объекта представлена на рисунке 2.

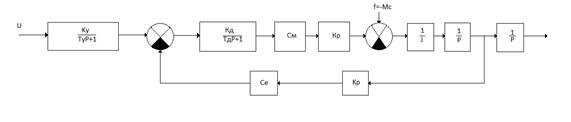
Рисунок 2. Структурная схема одноканального электромеханического объекта

Усилитель мощности представлен апериодическим звеном. Электродвигатель – апериодическим и двумя пропорциональными звеньями. Редуктор – двумя пропорциональными звеньями. Кинематический механизм – двумя интегрирующими звеньями и одним пропорциональным звеном с коэффициентом . Для проведения соответствующего математического моделирования работы  манипулятора (рисунок 2) был использован пакет прикладных математических программ Scilab, приложение Xcos [1]. Таким образом, модель  одноканального электромеханического объекта может быть представлена в виде, изображенном  на рисунке  3.

Рисунок 3. Модель привода

Результат проведённого моделирования представлен на рисунке 4.

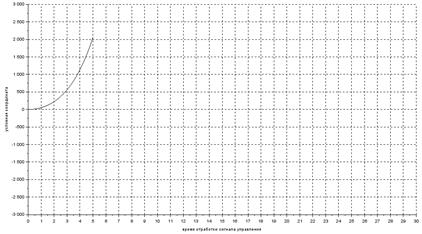
Рисунок 4. Графическое окно с симуляцией работы одноканального электромеханического объекта

Средствами микроконтроллерной платформы Arduino (аппаратным и программным обеспечением) получен рабочий скетч для управления манипулятором, лабораторный макет которого изображён на рисунке 7.

Arduino – набор аппаратно-программных средств, для построения систем автоматики и робототехники, программной частью которого является объектно-ориентированный язык программирования C++, а аппаратная часть представляет собой набор смонтированных печатных плат [3].

Программная часть состоит из бесплатной программной оболочки (IDE) для написания программ, их компиляции и программирования аппаратуры (рисунок 5).

Рисунок 5. Окно программной оболочки Arduino IDE

Аппаратная часть представляет собой набор смонтированных печатных плат, продающихся как официальным производителем, так и сторонними производителями (рисунок 6).

Рисунок 6. Arduino Uno R3

Исследование работы макета в различных режимах подтвердило правильность результатов математического моделирования.

Средства симуляции лабораторного макета с учётом динамических и кинематических особенностей позволяют получить осциллограмму переходных процессов [2, с. 162].

Рисунок 7. Лабораторный макет манипулятора на базе Arduino

Зная их характеристики можно подбирать наиболее оптимальные режимы работы одноканальной электромеханической системы, исследовать их на макете для того, чтобы полученные результаты использовать при проектировании реальных объектов.