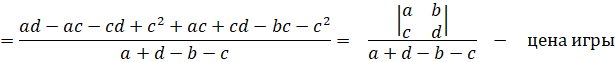Вычисление равновесия в матричной игре вида 2 х 2

Матричная игра – это парная игра, которая задается набором чистых стратегий  и    первого и второго игроков, а также платежной матрицей  , определяющей выигрыш первого игрока при выборе игроками стратегий i и j соответственно. Целью первого игрока является максимизация своего выигрыша, а целью второго – минимизация выигрыша противника.

Если седловая точка в платежной матрице отсутствует, то решения в чистых стратегиях не существует. В таких случаях ищут решение игры в смешанных стратегиях.   

Критерий существования равновесия в смешанных стратегиях матричной игры вида 2*2.

У каждого из двух игроков есть ровно две чистые стратегии.

Для того чтобы матрица 2*2 имела равновесие в смешанных стратегиях необходимо и достаточно, чтобы одна из её диагоналей доминировала над другой, т.е. каждый элемент одной диагонали строго больше, чем каждый элемент другой диагонали.

либо

Доказательство.

Необходимость. Пусть в матрице одна из диагоналей доминирует над другой. Покажем, что в ней нет равновесий только в смешанных стратегиях, т.е. седловой точки нет.

Седловой точки нет.

Достаточность. Если в матрице нет седловой точки, то одна из диагоналей доминирует надо другой.

Пусть 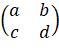   не имеет седловой точки.

Покажем, что одна из диагоналей доминирует над другой.

Если в матрице нет седловой точки, то в ней не может быть двух одинаковых элементов.

Покажем, что в такой матрице есть седловая точка.

В матрице   седловой точки нет.

Выделим min элемент в 1-ой строке.

Значит,  

Анализируем столбцы:  

Главная диагональ доминирует над второй диагональю.

ч.т.д.

Вычисление равновесных смешанных стратегий для матрицы вида 2*2

Пусть дана матрица  

В данной матрице одна из диагоналей доминирует над другой => в данной матрице есть равновесие в смешанных стратегиях.

Рассмотрим две прямые:

max точка этого семейства будет точка пересечения этих двух прямых.

Равновесная стратегия для первого игрока.