ПАРАБОЛА ТИПТЕГІ ДИФФУЗИЯ ТЕҢДЕУІН ДИФФЕРЕНЦИАЛ ЖУЫҚТАУ ӘДІСІ АРҚЫЛЫ МОДЕЛЬДЕУ (MATLAB)

Түйіндеме. Бұл мақалада диффузия теңдеуінің параболалық типіндегі дифференциалдық теңдеудің шешімі қарастырылады. Диффузия теңдеуінің шешімі дифференциалдық жуықтау әдісімен қарастырылады, оның негізінде диффузия теңдеуінің аппроксимациясын аламыз. Функцияны Тейлор қатарына бөлу арқылы біз уақыт кеңістіктік тордың орталық айырымдылық сұлбасын аламыз. Диффузия теңдеуінің шешімін алғаннан кейін біз Matlab ортасында функцияның графигін құрамыз.

Кілт сөздер: Дифференциял жуықтау әдісі, диффузия теңдеуі, Тейлор қатары.

Кіріспе. Диффузия теңдеуі дербес дифференциалдық теңдеудің белгілі бір түрі болып табылады. Ол тұрақты емес және стационарлық. Түсіндіру мағынасында диффузиялық теңдеуді шешу кезінде біз заттың (немесе басқа заттардың) концентрациясының кеңістіктік координаттар мен уақытқа тәуелділігін табу туралы айтып отырмыз және коэффициент беріледі. Қозғалыстағы сұйықтар мен газдардағы диффузия немесе жылу өткізгіштік мәселелерінде диффузия теңдеуінің орнына макроскопиялық қозғалысты елемеу мүмкін болмайтын жағдайға диффузия теңдеуін кеңейтетін тасымалдау теңдеуі қолданылады. Осы теңдеулердің шешімін өз еңбетерінде қарастырған Қазақстандық ғалымдар -  М.Бөріханов, М.Муратбекова, және жетекшілік етіп отырған П.М. Пирниязова өз еңбектерінде рекуррент -оператор әдісі мен қарастырған [1,2,3].    

Мәселенің қойылуы.  Берілген дербес туындылы диффузия дифференциал теңдеуін бірінші дифференциал жуықтау әдісі мен аппроксимациясын алуын қарастырайық [1]

                                                                                                          (1)

Бұл жерде  - диффузия коэффициенті, /с , - адсорбцияланатын ағынның көлемдік шығыны, /с

Шешу әдістері.  Дифференциалды жуықтау әдісі – белгілі шамаға жақын функцияның мәні. Әдіс функцияның графигін жуықтау үшін белгілі функция мәніндегі тангенсті пайдаланады. Дифференциалды жуықтау деп аталатын бұл әдіс уақыт бойынша жүйенің х шығысын дифференциалдауды талап етеді. Айырмашылық немесе дифференциалды жуықтау әдістерінің бірнеше елеулі шектеулері бар болса да, олар қажет болған жағдайда квазисызықтыру процедурасы немесе градиент типті процедура үшін бастапқы жуықтауды есептеу үшін пайдаланылуы мүмкін. Алгоритм итеративті емес, шешім бірінші итерацияда алынады. Алдымен айырмашылықты жуықтау деп аталатын алгоритмнің дискретті нұсқасын қарастырайық, содан кейін дифференциалды жуықтаудың үздіксіз жағдайын қарастырамыз. Алгоритм өте қарапайым және оны көптеген авторлар бірнеше рет қарастырған, бірақ оның қазіргі түсіндірмесі бойынша алгоритмнің негізгі жасаушысы Ричард Беллман екені жалпы мойындалған.

                                                                                                          (1’)

Дифференциал әдісі  - теңдеулерді шешуде қолданылатын дискреттеу үздіксіз аймақты оқшауланған нүктелер жиынтығымен ауыстыру болып табылады. Туындыларды дифференциал әдісімен ауыстыра отырып диффузия теңдеуінің шешімін бастапқы теңдеуді шешуге дейін жақындатамыз. Туындыларды дифференциал әдісімен жуықтау идеясын жақсы түсіну үшін, u(t,x) функциясының (t,x) нүктесіндегі туындысының анықтамасын айтамыз

=                                                                                                     (2)

Егер u(t,x) функциясы үздіксіз, ал  – жеткілікті аз болса, онда []/ айырымдылық мәні  туындысының мәніне жақын болады.

Айырымдылықтың дұрыстығын   функциясын Тейлор қатарына / нүктесі бойынша, туындыларға жуықтау арқылы тексеруге болады.

                                                          (3)

Мұнда «Оң жақ айырымдылық» формуласы берілген:

                                                                                (4)

 - туынды жуықтылар арқылы шексіз шекті айырымдылықты құруға болады.

                                                      (5)

Бұл формулада «Сол жақ айырымдық» формуласы берілген.

                                                                           (6)

Енді  «Оң жақ айырымдылық» формуласы мен  «Сол жақ айырымдық» формуласын Тейлор қатары бойынша  нүктесінде жайылмасын (4) және (6) қосып, орталық айырымдылық формуласын аламыз

                                                                                        (7)

Бұл жерде   - «туындыны жуықтау қателігі».

 және  нүктелеріндегі туындыларында Тейлор қатарына жаямыз.

                                                                                  (8)

                                                                                           (9)

Осылайша Тейлор қатарына жайылған диффузия теңдеуін жинақтаймыз.

                                                                 (10)

Matlab қосымшасында диффузия теңдеуінің орындалу процедурасы

clc

clear

close all

nx = 3; nt = 3; s = 0; v = 1;  t0 = 0;

 tf = 0.2;

   dx = (v-s)/(nx-1);

   dt = (tf - t0)/(nt-1);

    x = s:dx:v;

t = t0:dt:tf;

a = -dt/dx^2

b = 1+ (2dt/dx^2)

%% Analytical Solution

UA = zeros (nx, nt);

 for j = 1: nt

 for i = 1:nx

        UA(i,j) = sin(pi*x(i))*exp(-pi^2)*t(j);

    end

end

figure()

  contourf (UA,200,'linecolor','non')

     Xlabel('x')

       Ylabel('t')

         title('Analytical solution')

           colormap(jet(256))

            colorbar

              caxis([0,1])

                %%Numerical Solution

      UN =  zeros (nx, nt);

         %%Initial condition

             UN (1,:) = sin(pi*x(i));

       %%for j = 1: nt - 1

         %%for i = 1:nx - 1

           %%UN(i,j) = a*UN (i+1,j-1)+ b*UN(i+1,j) + a*UN(i+1,j+1)

    %%end

%%end

 %%figure()

   %%contourf (UN,200,'linecolor','non')

    %%xlabel('x')

     %%ylabel('t')

       %%title('Numerical solution')

      colormap(jet(256))

    colorbar

  caxis([0,1])

Зерттеу нәтижесі: 0.834, =0.532  функциясындағы t=1, t=3, t=5с. уақыт ішінде [1,2] алған нәтижеміз. Алынған нәтиже басқа авторлар нәтижесімен салыстырғанда Matlab пакетінде есептеулер жүргізілуі өте тиімді және тез. 

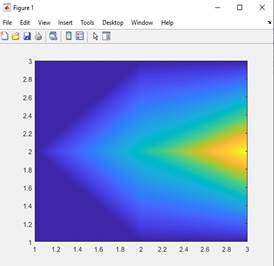
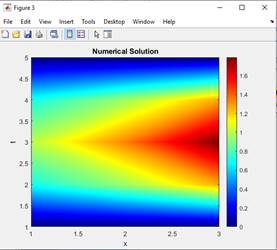
Сурет 1. Бірөлшемді диффузия теңдеуінің      Сурет 2. Бірөлшемді диффузия теңдеуінің

таралуы                                                                        жүруі

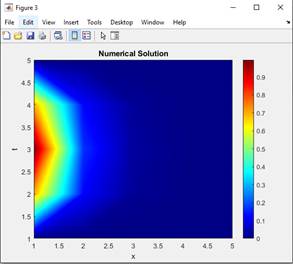
Сурет 3. Бірөлшемді диффузия теңдеуінің

таралуы

Берілген  суреттерде диффузия теңдеуінің MATLAB пакетіне салғанда, 1, 3, 5 секунд ішінде бөлменің көлеміне сәйкес будың біркелкі таралуы.  

Талдау. 0.834, =0.532 функциясындағы t=1, t=3, t=5с. уақыт ішінде [1,2] алған нәтижеміз. Алынған нәтиже Андрей Анатольевичтің «Численные методы решения уравнения диффузии в системе MATLAB»  нәтижесімен салыстырғанда Matlab пакетінде есептеулер жүргізілуі өте тиімді және тез.  

Қорытынды. Жоғарыда қарастырылған диффузия дифференциал теңдеуін Бірінші диффернциал жуықтау әдісімен шешімі қараСТЫРЫЛДЫ,  қойылған мәселенің шешімі Matlab қосымша қолданбалы пакетінде алынды. Атап айтқанда,  осы пакеттің басқа пакеттерден ерекшелігі MATLAB программалау тілі интерпретаторлар класына жатады. Бұл жүйенің кез келген пәрмені оның аты (идентификаторы) бойынша танылады (түсіндіріледі) және кез келген бағдарлама кодының бөліктерін оңай тексеруді қамтамасыз ететін пәрмен жолында дереу орындалатынын білдіреді. Сонымен бірге MATLAB программалау тілінің интерпретациялық сипаты осы жүйенің құралдарын сипаттаудың бірінші жолдарынан бастап оның программалау тілі іс жүзінде сипатталғанын білдіреді. Жүйенің маңызды артықшылықтары оның ашықтығы мен кеңеюі болып табылады.