ОЦЕНКА ПОКАЗАТЕЛЯ ЛИПШИЦА В ОСОБЫХ ТОЧКАХ СИГНАЛА

Аннотация. В статье представлен метод для нахождения и классификации особых (сингулярных) точках сигнала – точках, где сигнал теряет свою гладкость какого-либо порядка.

Ключевые слова: показатель Липшица, исследование сигналов, сингулярные точки, вейвлет-преобразование.

При изучении различных сигналов особое внимание обращают на точки, в которых сигнал теряет свою гладкость. В этих точках, как правило, содержится полезная информация об этом сигнале. К примеру, в двумерных сигналах (изображениях), особые точки показывают наличие границ между объектами.

Помимо поиска таких точек, важно знать, на сколько сильно сигнал в этой точке потерял свою гладкость. Показатели Липшица в математике чаще всего связываются с понятием гладкости и регулярности функции, а показатель Липшица в точке будет говорить о локальной регулярности сигнала в этой точке.

Обычно для оценки показателя Липшица всего сигнала или на каком-то его участке можно использовать преобразование Фурье, но оно совсем не подходит для оценки показателя в точке. С этой проблемой поможет справиться вейвлет-преобразование, так как оно дает возможность изучить сигнал одновременно и во временной и в частотной области.

«Вейвлет» - функция, чей интеграл по всей числовой прямой равен нулю, так как интеграл до нуля и после нуля равны по модулю и противоположны по знаку. Вейвлет-преобразованием функции f(x) будем называть свертку этой функции с некоторой вейвлет-функцией ψ(x), которая может быть расширена с каким-либо масштабом s. Формула вейвлет-преобразования выглядит следующим образом:

  [1, с.618]

Заметим, что функции f(x) будем брать из Гильбертова пространства функций .

Функция f(x) называется Липшицевой с показателем α (n ≤ α ≤ n+1, n ℕ) в точке , если существует константы A и >0, полином степени n , и для любого h < выполняется:

 [1, с.619]

Липшицевость функции – ее более обобщенная мера дифференцируемости.

Введем понятие максимума модуля вейвлет-преобразования, как пар значений (s, x), таких, что для некоторого s вейвлет-преобразование имеет локальный максимум по переменной x. Также в пространстве точек (s, x) любую связную прямую из точек максимума модуля будем называть линией максимума.

Теоремы из [1, c.621-623] гласят, что если найдется линия максимума, содержащая точку (s, x) = (1, ), то точка  – особая, и для всех точек максимума модуля, лежащих на линии выполнено:  для некоторого положительного A и любого масштаба s, если для него есть точка на линии максимумов.

Прологарифмировав полученное неравенство узнаем, что наилучшая оценка  – угол наклона прямой, аппроксимирующей зависимость логарифма от вейвлет преобразования от масштаба s в точках линии максимума. Для подсчета угла наклона прямой воспользуемся методом наименьших квадратов.

Итак, теперь нам известен алгоритм нахождения показателя Липшица в особых точках сигнала. Но обнаружим мы сингулярность или нет, зависит от используемого вейвлета, а вернее от количества его нулевых моментов. Количество нулевых моментов равное n – это свойство вейвлет-функции, которое означает равенство нулю интеграла по всей числовой прямой от произведения вейвлета на , где k < n . Известно, что вейвлет с 1 нулевым моментом может обнаружить сингулярность только 1 порядка, с 2 н.м. – сингулярности 1 и 2 порядка и т.д.

Приведем пример описанного ранее способа. Возьмем функцию f(x) с двумя сингулярностями разного порядка (1 и 2) в двух разных точках, применим к ним вейвлет-преобразования с вейвлетами (gaus1, gaus2) и посмотрим на линии максимумов в этих точках, а также найдем значение показателя Липшица в этих точках. Видим, что вейвлет gaus1 обнаружил только сингулярность 1 порядка в точке 9, а gaus2 две сингулярности в точках 9 и 14. Подсчитав показатель Липшица в этих точках при помощи МНК, получим значения 0.98 и 1.98 соответственно. Пример реализован на языке Python при помощи библиотеки PyWavelets [2]

Рисунок 1. f(x)                     Рисунок 2. Максимумы, gaus1

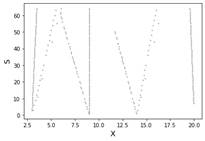
Рисунок 3. Максимумы, gaus2                      Рисунок 4. МНК

Заключение. Подведем итог работы. Продемонстрирован способ при помощи максимумов модулей вейвлет-преобразования функции найти ее особые точки, а также посчитать значение локальной регулярности в этих точках. В подтверждение показан пример функции с двумя сингулярностями разного порядка, которые обнаружились при помощи описанного способа, а также посчитано значение показателей Липшица в найденных точках.