CUBIC EQUATIONS

Consider the general concept of n-degree polynomials according to the textbook by E.B. Vinberg [1, p. 5].

Definition [1]: a polynomial of n-degree is a function of the form:

,                                                                               (1)

where  – are real numbers (some of them may be zero). The numbers  in equation (1) are called the coefficients of the function  at . A polynomial whose coefficients are all equal to zero is called zero.

Cubic equations are polynomials of the third degree, having the form:

,                                                                                    (2)

where  – are real numbers, with .

Equally important is the concept of a reciprocal equation. The reciprocal equation is an equation of the form:

, 

where [1].                               

Consider properties for polynomials of the third degree.

The commutativity and associativity of addition follow from the validity of these properties for the addition of numbers, since the coefficients are added at each degree of the unknown separately [2].

The commutativity of multiplication follows from the commutativity of multiplication of numbers and the fact that in the definition of the product of polynomials the coefficients of both factors  and  are used equally.

The associativity of multiplication of polynomials is proved as follows: if, in addition to the polynomials written above, a polynomial  is given: , then the coefficient at , where , in the work  will serve as a number =, and in the work  - its

equal number =.

Finally, the validity of the distributivity law follows from the equality

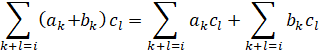
Since the left side of the equality is the coefficient of in the polynomial , and the right side is the coefficient of the same degree of the unknown in the  [2].

Note that the role of unit in the multiplication of polynomials is played by the number 1, considered as a polynomial of degree zero.

 On the other hand, a polynomial  has an inverse polynomial , if and only if

=1,                                                                                                       (3)

if is a polynomial of degree zero. Indeed, if is a non-zero number , then the inverse polynomial for it is the number . If has , then the degree of the left side of the equality , if the polynomial existed, would be at least n, while on the right there is a polynomial of degree zero [3, p. 133]. This implies that for the multiplication of polynomials, the inverse operation - division - is impossible.