ОПТИМИЗАЦИЯ УЧЕБНОГО РАСПИСАНИЯ С ИСПОЛЬЗОВАНИЕМ ЦЕЛОЧИСЛЕННОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Аннотация. Составление учебного расписания представляет собой сложную задачу комбинаторной оптимизации, особенно при наличии множества ограничений: доступности аудиторий, занятости преподавателей и предпочтений студентов. В данной работе реализована модель целочисленного линейного программирования (ЦЛП) для оптимизации расписания академических занятий. На основе данных одного из факультетов университета вручную была собрана сводная таблица дисциплин, преподавателей, групп и аудиторных требований. Решение модели осуществлялось в Excel с применением надстройки Solver. Были учтены как жёсткие, так и частично удовлетворяемые условия.

Ключевые слова: оптимизация; линейное программирование; прикладная математика; целочисленная модель; учебный процесс.

Автоматизация планирования учебного процесса требует применения строгих математических методов, способных учитывать одновременно множество условий. Традиционный ручной подход к составлению расписаний не гарантирует отсутствие конфликтов и не оптимален по количеству так называемых «окон» — пустых пар у студентов [1].

Математическое моделирование позволяет формализовать задачу и свести её к задаче линейного программирования. Применение формальных методов в образовательной среде позволяет систематизировать нагрузку и минимизировать ошибки в планировании [4].

Для решения задачи использовалась бинарная целочисленная модель. Каждая переменная x_ijk ​ обозначает, запланирована ли дисциплина i для группы j в временной слот k. Переменные принимают значение:

x_ijk​=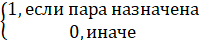 

Целевая функция:

minZ=общее количество конфликтов + «окон» + отклонений от предпочтений

Система ограничений включала:

• не более одной дисциплины в один слот для каждой группы;
• запрет на одновременную занятость преподавателя в двух местах;
• учёт вместимости и специализации аудитории;
• соблюдение недельного распределения по учебному плану [5].

Модель была построена вручную в Excel, где каждая переменная — это отдельная ячейка, принимающая 0 или 1. Ограничения задавались через интерфейс Solver [3].

В ходе анализа качества расписания были рассчитаны следующие показатели:

• Число конфликтов (одновременных назначений преподавателя): 0 — удалось полностью исключить логические ошибки.
• Среднее количество "окон" (пустых слотов) у студентов: 0.6 на группу в неделю, что соответствует хорошему уровню планирования [2].
• Число случаев превышения вместимости аудитории: 0 — корректный учёт характеристик помещений.
• Процент удовлетворённых предпочтений преподавателей: 92% — большая часть пожеланий соблюдена, остальные не нарушали жёстких требований.

Также выявлено: дисциплины с ограниченным числом преподавателей оказывают наиболее сильное влияние на перегрузку слотов.

На рисунке 1 была представлена визуализация распределения «окон» (пустых пар) по группам.

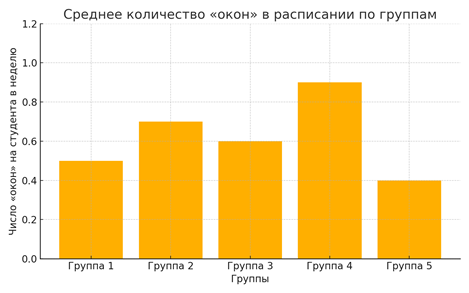
Рисунок 1. Среднее количество «окон» в расписании по учебным группам