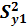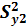Эконометрическая модель зависимости среднегодовой численности занятых в сфере образования от среднемесячного уровня заработной платы

Аннотация. Данная статья посвящена исследованию на тему влияния среднемесячного уровня заработной платы в сфере образования на число занятых в этой сфере. Проблема оплаты труда одна из трудноразрешимых проблем, которая затрагивает не только экономическую сферу, но и социальную и политическую.

Ключевые слова: образование, занятость, заработная плата.

Существует мнение, что в России рост заработной платы сотрудников образовательных учреждений не приведет к повышению качества работы учителей, поскольку школьным сообществом это воспринимается как справедливый возврат накопленного за долгие годы долга. Кроме того, рост заработной платы учителей воспринимается ими как увеличение учебной нагрузки, поэтому снижается привлекательность данной профессии.

Теперь стоит рассмотреть ситуацию на практике, опираясь на статистические данные, предоставленные Федеральной службой государственной статистики. А именно, проанализировать влияние фактора X (среднемесячная номинальная начисленная заработная плата в сфере образования) на результативный показатель Y (среднегодовая численность занятых в сфере образования). Периодом исследования является 2005 – 2016 гг.

Для достижения поставленной цели будут выполнены следующие задачи:

• Составить спецификацию,

• Проверить правильность выявленного тренда, качественность и гетероскедастичность модели.

Практическая часть

Составление спецификации

По исходным данным (Таблица 1) строится точечная диаграмма рассеивания для определения линии тренда (Рисунок 1).

Таблица 1

Исходные данные

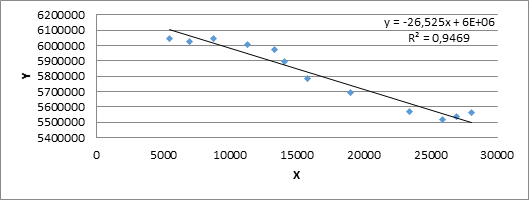
Рисунок 1. Диаграмма рассеивания

По результатам точечной диаграммы можно отметить, что направленная вниз линия тренда говорит о том, что в целом за изучаемый период наблюдается отрицательная тенденция: с ростом заработной платы снижается количество занятых в сфере здравоохранения.

В парной регрессии спецификация задается в виде изолированного уравнения:

Y_t= a₀+ a₁*X_1t+ e_t

С помощью функции ЛИНЕЙН в MS Excel производится оценка матрицы методом наименьших квадратов (Таблица 2).

Таблица 2.

Линейная

Оцененная спецификация приобретает вид:

Yt= 6246162-26,5252*X_1t+ e_t

Коэффициент детерминации равен 0,9469. Это значит, что изменение величины заработной платы в модели объясняет изменение числа занятых в сфере образования на 94, 69%.

Проверка выявленного тренда с помощью метода «сравнение средних уровней ряда»

Первым этапом для проверки наличия выявленного тренда является деление исходного временного ряда на две равные части по числу уровней (n₁+n₂=n).

Далее определяем значение дисперсии для обеих частей ряда при помощи функции ДИСПРА в MS Excel. Полученные значения дисперсий представлены в таблице 3.

Таблица 3.

Значение дисперсий

Чтобы проверить гипотезу о равенстве (однородности) дисперсий обеих частей ряда, используется F-критерий Фишера. Для вычисления F-критерия большую дисперсию делят на меньшую:

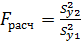 = 1,1479

Также, определяется F_кр по формуле FРАСПОБР. В исследуемой модели F_кр=4,9646.

Так как F_расч < F_кр, то с заданной вероятностью (0,05) нет оснований отвергать нулевую гипотезу о равенстве дисперсий обеих частей ряда.

Далее проверяем основную гипотезу о равенстве средних значений с использованием t-критерия Стьюдента:

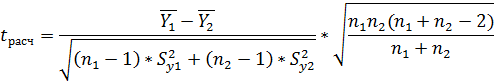
С помощью функции СТЬЮДРАСПОБР определяется t_кр=2,2281

Так как 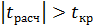, то можно сделать вывод о том, что в исследуемой модели тренд присутствует.

Проверка модели на качественность

Для начала, чтобы проверить модель на качественность, необходимо оценить значение коэффициента детерминации. В исходной модели R² = 0,94685449, что свидетельствует о среднем уровне зависимости.

Для более точного определения качественности проведем F-тест.

С помощью функции ЛИНЕЙН в MS Excel ранее было рассчитано значение F = 178,1626.

C помощью функции FРАСПОБР(0,05;1;10) рассчитывается значение Fкр = 4,9646.

Поскольку F>>Fкр, то можно смело признавать спецификацию качественной.

Тест Голдфелда-Кванта на гетероскедастичность

Для проведения теста Голдфелда-Кванта необходимо сначала сортировать исходные данные по фактору X по возрастанию. После чего – разбить на 3 равных диапазона. В начальном и конечном диапазонах вычислить значение дисперсии ESS при помощи функции ЛИНЕЙН (Таблица 4).

Таблица 4

ESS для начального и конечного диапазона

После нахождения дисперсий определяется значение GQ:

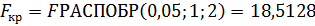
Так как GQ < F_кр (0,5913 < 18,5128), то можно говорить о том, что гетероскедастичность в модели отсутствует, то есть наблюдение однородно.

В ходе работы была составлена модель зависимости среднегодовой численности занятых в сфере образования от среднемесячного уровня заработной платы в соответствующей сфере. Были проведены тесты для проверки данной спецификации на качественность и гетероскедастичность, а также осуществлена проверка выявленного тренда. Спецификация успешно прошла все тесты.

Однако, была выявлена следующая закономерность: с увеличением заработной платы снижается численность занятых в сфере образования, что выбивается из логики. Ведь должно быть наоборот, если зарплата растет, то и спрос на данную профессию должен расти.

В данном случае важно понимать, что на заинтересованность в такой профессии как воспитатель, учитель, преподаватель влияет множество других факторов. Например, это социальная, культурная и политическая обстановка как в стране, так и на территории ее субъектов.

Чтобы достичь более точных результатов, необходимо ввести большее количество переменных и провести более детальный анализ.