Решение текстовых задач на умножение и деление обучающимися младших классов
Журнал: Научный журнал «Студенческий форум» выпуск №2(53)
Рубрика: Педагогика

Научный журнал «Студенческий форум» выпуск №2(53)
Решение текстовых задач на умножение и деление обучающимися младших классов
Аннотация. В данной статье рассматривается значимость решения текстовых задач на умножение и деление в начальной школе. Результат будет зависеть от того, как усвоили дети конкретный смысл действий умножения и деления. Рассматриваются методические подходы решения текстовых задач. Раскрываются содержание и способы обучения, по программе «Перспективная начальная школа» во 2 классе. На проверку уровня сформированности смысла умножения и деления младших школьников. При проведении данного педагогического исследования был проведен опрос в виде тестирования.
Ключевые слова: умножение, деление, смысл действий, текстовая задача.
Решение текстовых задач в начальной школе является основой успешного усвоения способов и приемов математических действий. В начальной школе очень важно уметь решать задачи разного вида, которые расширят возможности учеников в будущей учебной деятельности.
Решая, текстовые задачи дети приобретают необходимые знания, умения и навыки. Так, сюжеты задач, отражающие практические ситуации, могут быть знакомы детям из их жизненного опыта. Это помогает ему осознать реальные количественные отношения между различными объектами (величинами) и тем самым углубить и расширить свои представления о реальной действительности.
Обучением детей, решению текстовых задач, занимались такие методисты, как М.И. Моро, М.А. Бантова, С.Е. Царева, Н.Б. Истомина [1]. В их публикациях предложено немало практических приемов, облегчающих поиск решения задачи. Однако теоретические положения о нахождении оптимальных путей обучения младших школьников решению текстовых задач разработаны недостаточно. В каждом классе найдутся дети, которые испытывают затруднения при решении текстовых задач, в том числе и задач на умножение и деление.
Первоначальным этапом для успешного решения таких задач является усвоение и понимание детьми смысла умножения и деления. Знакомство и изучение этого смысла в большинстве школьных программ начинается со 2 класса. Рассмотрим, как это происходит на примере УМК «Перспективная начальная школа».
Наиболее существенной особенностью учебно-методического курса «Математика» автора А. Л Чекина [4] является содержание курса, которое представлено в пяти основных линиях: арифметической, геометрической, величинной, алгоритмической (обучение решению задач) и информационной (работа с данными). Значительная роль уделяется изучению геометрического материала и изучению величин.
Суть предмета постигается через естественную связь математики с окружающим миром, т.е знакомство с тем или иным математическим понятием осуществляется при рассмотрении конкретной реальной или псевдореальной (учебной) ситуации.
Итак, простые текстовые задачи на умножение и деление вводятся во 2 классе при раскрытии конкретного смысла действия умножения и деления.
Для раскрытия смысла умножения предлагаются упражнения на вычисление одинаковых слагаемых, определив каждое слагаемое в сумме, дается вариант этой записи по-другому – в виде произведения. Далее дети уже учатся заменять суммы с одинаковыми слагаемыми произведениями. Имеются задачи с иллюстрациями на умение записывать решение задачи в виде суммы и произведения.
Автор учебника использует также обратные задания, на понимание и осознание учащимися выполняемых действий, например, составляют задачу, решением которой будет определенное произведение.
Для раскрытия смысла деления по содержанию, с которым дети знакомятся во второй части учебника 2 класса, предлагаются задания на распределение предметов. На проверку усвоения нового знака, есть специальные задания.
Так же дети усваивают новое понятие и учатся правильно читать выражение со знаком деления. Каждое новое понятие закрепляется заданием, например, «Запиши частное следующих чисел: 8 и 4, 21 и 7, 36 и 6, 100 и 10, 72 и 8». Решение записывается в виде частного: 8:4, 21:7, 36:6, 100:10, 72:8. Учитель поясняет, что в этом случае запись выполняется с помощью нового знака «делить».
Далее следует знакомство с понятиями «делимое» и «делитель», которые подкрепляются иллюстрацией. И в конце также даются задания на понимание и проверку знаний о делении.
Нами был составлен и проведен тест уровня сформированности смысла умножения и деления младших школьников в силу отсутствия единых стандартизированных методик диагностики по данной теме, на базе БОУ г. Омска «Гимназия №19». В исследовании приняли участие 24 учащихся 3 класса, обучающихся по программе «Перспективная начальная школа».
Задания проверяли сформированность у учащихся следующих умений:
- заменять умножение сложением;
- заменять сложение умножением;
- вычислять значение произведения чисел;
- вычислять значение частного чисел;
- определять множители, если известно, что произведение равно 54;
- определять значение частного, если известен ответ равный 9;
- определять то, на какое число надо разделить 81, чтобы получилось 9;
- определять множители;
- сравнивать.
Содержание заданий определяется необходимыми видами упражнений, направленных на формирование умения решать текстовые задачи на умножение и деление, с которыми дети должны были познакомиться во 2-3 классах.
Результаты теста показали, что успешнее всего дети справились с заданиями на вычисление значение произведения чисел (100%), на замену умножения сложением (95%), вычислять значение частного чисел (95%), на определение в виде произведения каких чисел можно представить определенное число (91%), а так же на определение значения множителей при известном произведении (91%). Многие учащиеся допустили ошибки при сравнивании примеров с разными арифметическими действиями (87%), при определении значения частного каких-либо чисел, когда известно делимое или делитель (79%) и при определении того на какое число надо разделить частное, чтобы получить соответствующий делитель или делимое (79%). Самым сложным для учащихся оказалось задание на замену сложения умножением (справилось с этим заданием только 37%).
Проиллюстрировать результаты выполнения Теста можно с помощью следующей диаграммы (рис. 1).
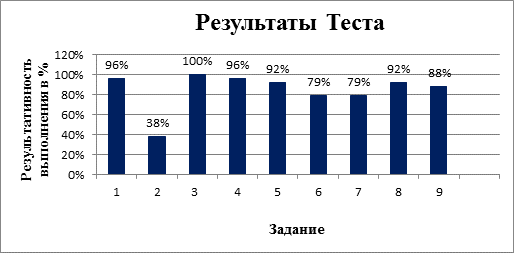
Рисунок. 1 Результаты выполнения Теста
Таким образом, результаты теста позволяют сделать вывод о готовности учащихся 3 класса к дальнейшему формированию умения решать простые текстовые задачи на умножение и деление по программе «Перспективная начальная школа».

