Алгоритм Fast-SLAM: фильтр частиц и байесовский подход

Метод одновременной навигации и картографирования (SLAM –  Simultaneous Localization and Mapping) является одним из наиболее актуальных подобластей робототехники. Понятие процесса SLAM на интуитивном уровне можно представить на простом примере.

Представим простой мобильный робот, оснащенный набором колес, соединенных с двигателем, и камерой. Такой небольшой набор представляет собой физическое устройство, способное изменять скорость и направление движения. Допустим, что наш робот управляется удаленно. Приводы позволяют роботу перемещаться, а камера обеспечивает достаточную визуальную информацию для оператора, чтобы понять, где находятся окружающие объекты и как робот ориентирован по отношению к ним. То, что делает человек – оператор – это пример SLAM.

Существует множество алгоритмов реализации метода SLAM, отличающихся друг от друга использованием разных аппаратных средств и алгоритмов вычислений. 

Общая постановки задачи всех методов SLAM следующая: вычисление оценок локализации робота и ориентиров на строящейся карте путем обработки данных, считываемых с датчиков.

Наиболее распространенными из них являются Vision SLAM (V-SLAM), Distributed Particle SLAM (DP-SLAM), Extended Kalman Filter SLAM (EKF-SLAM) и Fast-SLAM.

Алгоритм Fast-SLAM отличается от остальных вышеуказанных алгоритмов, так как является гибридным методом, в котором сочетаются методы DP-SLAM на основе фильтра частиц и метод EKF-SLAM, основанный на применении фильтра Калмана.

В данной работе будет рассмотрен фильтр частиц и байесовский подход в алгоритме Fast-SLAM.

В алгоритме Fast-SLAM фильтр частиц используется для построения карты окружающей робота среды путем взвешивания частиц.

Частицами в данном фильтре принято считать набор точек, которые представляют собой препятствия, встречающиеся на пути мобильного робота.

Фильтр частиц

Фильтр частиц – алгоритм, который приближается к заданному распределению с дискретной плотностью вида:

.

Данный алгоритм в результате его применения приводит к числовым рекурсиям. Фильтр частиц отличается от других фильтров похожей структуры, например, от фильтра масс (The Point Mass Filter), наличием стохастической сетки  (в фильтре масс предполагается детерминированная сетка), которая изменяется со временем. В большинстве стохастическая сетка более эффективна для представления пространства состояний. Фильтр частиц нацелен на оценку всей траектории, то есть он генерирует набор , где , состояний из N разных траекторий и оценивает его. Байесовское решение для вычисления заданного распределения вектора состояния имеет следующий вид:

.

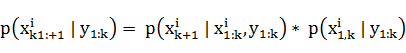Новая сетка в фильтре частиц получатся путем отбора частиц, имеющих определенный вес. Идея заключается в том, чтобы ввести плотность распределения . Теперь необходимо сгенерировать распределение случайным образом для каждой частицы, а затем нормализовать вес получившихся частиц.

Повторная выборка является решающим шагом. Без передискретизации, фильтр частиц будет разбиваться на независимые элементы, приводящим к траекториям  с относительными вероятностями . В результате работы фильтра все относительные веса будут стремиться к нулю, кроме тех, значения  которых близки к единице. Фильтр частиц состоит из двух основных этапов:

1. Этап инициализация;

2. Этап цикла фильтрации.

В этапе инициализации происходит инициализация параметров фильтра, их настройка.

Этап цикла фильтрации содержит в себе три части:

3. Движение робота;

4. Измерения датчиков;

5. Отсев частиц.

Стоит обратить внимание на то, что вес частицы, равный единице, не является показателем точного положения объекта. Это лишь означает, что некоторая координата встречается намного чаще остальных. Повторная выборка использует данные прошлых вычислений, поэтому частицы с наибольшим весом останутся после передискретизации. [2].

Байесовский подход к FAST-SLAM

Fast-SLAM предлагает возможность представить проблему одновременной локализации и построения карты с точки зрения Байесовской сети [3]. Байесовская модель мира – это представление его в таком виде, в котором есть определенные «случайные переменные» – переменные, которые принимают разные значения с разными вероятностями в зависимости от значений, возвращаемыми другими случайными переменными. В результате получается дерево случайных переменных, которые зависят друг от друга и указывают вероятность существования того или иного состояния «мира». Такую сеть принято называть Байесовской сетью.

Условная независимость ориентиров – это то, что позволило фильтру Калмана сделать оптимальное предположение при обновлении предсказаний состояния и значений неопределенности (ошибки). Условная независимость в Байесовской сети определяется набором правил d-разделения (d-separation rules). Два узла графа называются независимыми друг от друга, если каждый путь между ними имеет d-разделение. Дадим  определение d-разделения.

Два узла направленного графа  и  называются d-разделенными, если для любого пути из  в  (направление ребер в этом случае принято не учитывать) существует такой промежуточный узел  (не совпадающий ни с , ни с ), что либо связь в этом узле последовательная или расходящаяся, и узел  получает значимость, либо связь сходящаяся и ни узел , ни какой-либо из его потомков значимости не получает. В противном случае узлы называются d-связанными [4].

Можем использовать следующие графы (рисунок 1), позволяющие понять условную зависимость при решении проблемы SLAM. На схеме слева иллюстрируется как наблюдения, произведенные роботом, подвержены влиянию случайных величин оценки положения робота и ошибке считанных данных датчика. Байесовская сеть справа представляет собой аналогичную сеть, но в этом случае учитывается фактическое положение робота, которое определяется из оцененного положения и ошибки её определения.

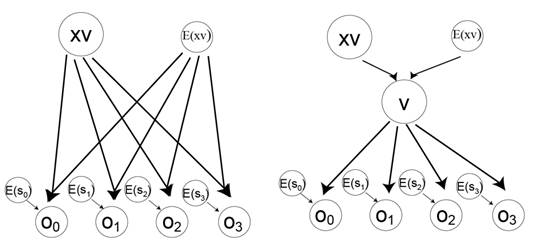
Рисунок 1. Условная зависимость в Байесовской сети

На рисунке 1 приняты следующие обозначения:

•  – оцененное положение робота;
•   – текущее положение робота;
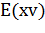•  – ошибка определения позиции робота;
•   – погрешность датчика;
•  – наблюдения, основанные на данных датчика.

Очень важным моментом в алгоритме SLAM является то, что мы не знаем точного положения робота, но понимание условной независимости признаков (меток, ориентиров),  учитывающих положения робота, достаточно для реализации алгоритма Fast-SLAM.