Корреляционный анализ валового сбора картофеля на примере Орловской области

CORRELATION ANALYSIS OF GROSS POTATO HARVEST ON THE EXAMPLE OF OREL REGION

Irina Filimonova

Student, Orel state agrarian University. N.V. Рarakhina, Russia, Orel

Natalia Yakovleva

Candidate of economic Sciences, associate Professor, Orel state agrarian University. N.V. Рarakhina, Russia, Orel

Аннотация. В данной статье мы проводим корреляционный анализ валового сбора картофеля с целью рассмотреть силу влияния посевной площади на валовой сбор картофеля.

Abstract. In this article, we carry out a correlation analysis of the gross potato harvest in order to consider the effect of the acreage on the gross potato harvest.

Ключевые слова: корреляционный анализ, валовой сбор, картофель, посевная площадь, регрессии, коэффициент эластичности, коэффициент детерминации, факторный признак, t-критерий Стьюдента.

Keywords: correlation analysis, gross harvest, potatoes, acreage, regression, elasticity coefficient, determination coefficient, factor feature, Student's t-criterion.

Корреляция – статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин [3]. По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака - низкие значения другого. При отрицательной корреляции соотношения обратные. При положительной корреляции коэффициент корреляции имеет положительный знак, например  r=+0,207, при отрицательной корреляции - отрицательный знак, например r=-0,207 [1].

Максимальное возможное абсолютное значение коэффициента корреляции r=1,00; минимальное r=0,00.

Общая классификация корреляционных связей

- сильная, или тесная при коэффициенте корреляции r>0,70;

- средняя    при 0,50<r<0,69;

- умеренная         при 0,30<r<0,49;

- слабая      при 0,20<r<0,29;

- очень слабая     при r <0,19 [2].

Произвести расчет по итоговым значениям можно по формуле:

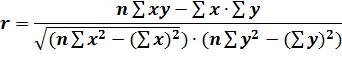                                                                                                (1)

С помощью корреляционного анализа определим влияние площади посадок картофеля, на валовый сбор по 9 годам. Для этого изобразим на графике зависимость валового сбора, от площади посадок, построим линейное уравнение регрессии, рассчитаем коэффициент корреляции и оценим его достоверность с помощью t-критерия Стьюдента.

Таблица 1.

Исходные данные

Построим график зависимости валового сбора картофеля от площади посадок картофеля (рис. 1).

Рисунок 1. Зависимость валового сбора от площади посадок картофеля

График показывает, что при уменьшении площади посадок картофеля, значение валового сбора картофеля в среднем понижается. В данном случае имеется линейная зависимость, которая может быть отражена уравнением регрессии:

где _х – теоретическое значение результативного признака;

а – параметр уравнения, который не имеет экономического смысла;

b – коэффициент регрессии [5];

х – факторный признак.

Таблица 2.

Данные для проведения корреляционного анализа

Для определения параметров a и b воспользуемся расчетными данными из таблицы 2 и решим систему двух уравнений, которая называется в статистике системой нормальных уравнений:

S y = an + bS x                                                                                                   (3)

S yx = aS x + bS x2

197.2 = 9a + 2685.2b

59346.29 = 2685.2a + 833087.98b

Решив систему уравнений получим:

a = 17.14

b = 0.02

Таким образом, уравнение будет иметь вид:

_х= 17.14+0.02х

Коэффициент b > 0, это подтверждает, что зависимость между посевными площадями картофеля и валовым сбором картофеля прямая. При увеличении площади на 1 га, валовой сбор картофеля в среднем увеличится на 0.02 ц/га.

Воспользовавшись формулой (57) r = 0.24. Коэффициент корреляции показал, что между изучаемыми факторами существует прямая зависимость. Причем, связь между факторами слабая.

Рассчитаем коэффициент эластичности:

Э = 0,02* 298.4 / 21.9 = 0,27 %

Коэффициент эластичности показывает на сколько процентов в среднем изменяется результативный признак при изменении факторного на 1 %. С изменением уровня посевных площадей на 1 % валовой сбор картофеля в среднем увеличится на 0,27 %.

Рассчитаем коэффициент детерминации по формуле:

D = 0,24² * 100% = 6%

Это означает, что зависимость очень слабая, в 6% случаев изменения посевной площади картофеля приведет к изменению валового сбора картофеля, остальные 94% вариации вызваны неучтенными в модели факторами.

Случайные ошибки параметром линейной регрессии и коэффициента корреляции определяются по формулам:

Подставив соответствующие данные в формулы 6-8 получим:

m_b=0.027; m_a=8.114=8.114; m_r=0.367

Рассчитаем t-критерий Стьюдента для каждого показателя (a, b, r), используя соответствующие формулы:

t_b=0.74; t_a=2.112; t_r=0.65

По специальной таблице установим табличное значение t-критерия Стьюдента. В нашем случае t_табл=2.3646 при уровне значимости 0.05 и числе степеней свободы n-2=9-2=7. Итак t_b t_табл;

t_at_табл; t_rt_табл. Следовательно, нулевая гипотеза о не существовании коэффициента корреляции и параметров регрессии отвергается т.е. a, b и r статистически незначимы.

Так так уравнение регрессии является статистически незначимым, расчет прогнозируемого значения валового сбора 1 т картофеля по данному уравнению не даст достоверного результата.