Обучение моделированию при решении текстовых задач в начальной школе

Одной из задач современного учителя начальных классов является формирование у младших школьников не только предметных, но и метапредметных умений, основу которых составляют универсальные учебные действия (далее – УУД). Моделирование как метапредметное умение относят к познавательным УУД, в частности, к общеучебным действиям, ведь моделирование является одним из ключевых видов деятельности человека, так как зачастую в той или иной форме предшествует любому делу.

Математика, как никакой другой предмет, позволяет формировать у обучаемых умения моделировать, схематизировать, работать с условными обозначениями, символами и знаками. В начальной школе с применением моделирования и схематизации решаются разнообразные текстовые сюжетные задачи. Каждый ученик начальной школы должен научиться кратко записывать условие задачи, иллюстрировать его с помощью рисунка, схемы или чертежа, обосновывать каждый шаг в анализе задачи и в ее решении, проверять правильность решенной задачи с опорой на составленную схему или чертеж [3].

Вспомним, что под моделированием понимается исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя.

Таким образом, основным понятием является понятие модели – упрощенного представления о реальном объекте, процессе или явлении. Под моделью также понимается объект, который отражает некоторые стороны изучаемого объекта или явления, существенных с точки зрения моделирования.

Основными этапами моделирования являются [1]: 1. Постановка задачи. На данном этапе определяется цель моделирования, а также проводится анализ исследуемого объекта. 2. Построение модели и ее апробация. 3. Анализ адекватности модели (проверка соответствия полученных результатов поставленным целям).

Рассмотрим на конкретном примере для обучающихся первого класса, каким образом реализуются этапы моделирования при решении младшими школьниками текстовых задач.

Задача. У Маши в вазе стоит 7 тюльпанов, а у ее подруги Юли на 2 тюльпана меньше. Сколько всего тюльпанов у девочек?

Любая текстовая задача представляет собой описание какого-либо явления, то есть эта задача уже представляет словесную модель рассматриваемого явления. Для ее решения обучаемые строят высказывательную модель задачи, а именно выявляют, о каких объектах идет речь в задаче, устанавливают исходные (известные) и подлежащие определению величины, определяют условия (утверждения) и требования, то есть вопрос, на который необходимо найти ответ.

Для данного примера высказывательная модель принимает следующий вид. 

• Объекты: тюльпаны.
• Утверждения: 1) У Маши 7 тюльпанов. 2) У ее подруги Юли на 2 тюльпана меньше.
• Требования: 1) Сколько тюльпанов у Юли? 2) Сколько всего тюльпанов у девочек?

Для решения задачи младшему школьнику необходимо составить ее математическую модель, в качестве которой могут выступать как уравнение, так и запись решения в виде выражения по действиям, как в данном случае. Если учащиеся начальной школы испытывают затруднения на этом этапе решения, то они прибегают к построению вспомогательных моделей: графических и знаковых.

К графическим моделям относятся:

- рисунок, изображающий реальные предметы (рис. 1). Использование рисунков как графических моделей характерно для первоначального этапа работы младших школьников с текстовыми задачами, на котором они только учатся действиям схематизации и моделирования;

Рисунок 1. Графическая модель: рисунок

- условный рисунок. На условном рисунке школьники изображают объекты, о которых идет речь в задаче, с помощью обозначений, символов, знаков, например: квадратов, треугольников, кружочков и др. (рис. 2);

Рисунок 2. Графическая модель: условный рисунок

- чертеж. На чертеже школьники изображают величины и отношения между ними с помощью чертежных инструментов (рис. 3);

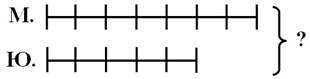
Рисунок 3. Графическая модель: чертеж

- схематический чертеж или схема (рис. 4) выполняется или с помощью чертежных инструментов, или от руки. На нем указываются все данные и искомые.

Рисунок 4. Графическая модель: схема

К знаковым моделям относятся краткая запись и таблица. Например, краткая запись в задаче о тюльпанах может быть представлена так же, как на рисунке 5.

Рисунок 5. Краткая запись задачи

Таблица как вид знаковой модели используется главным образом тогда, когда в задаче имеется несколько взаимосвязанных величин (например, стоимость покупки – цена – количество единиц товара).

Отметим, что рассмотренные знаковые и графические модели являются вспомогательными и не представляют модели самой задачи.

Математической моделью для рассмотренной текстовой задачи, как было отмечено ранее, может служить запись в виде выражения:

7 + (7 – 2) = 12 (т.) – всего тюльпанов у девочек;

или запись по действиям:

1) 7 - 2 = 5 (т.) - тюльпанов у Юли;

2) 7 + 5 = 12 (т.) - всего тюльпанов у девочек.

Ответ:12 тюльпанов.

При решении задачи от учеников часто требуется выполнить ее проверку путем составления и решения обратной задачи или с помощью установления соответствия между полученными значениями искомых величин и исходными данными. С одной стороны, этим действием обучающиеся проверяют правильность решения, а с другой, адекватность составленной модели.

Таким образом, решение текстовых задач позволяет формировать у младших школьников целый спектр метапредметных умений, связанных с моделированием [2]: схематизация объекта или явления; построение модели и ее преобразование; исследование модели; использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов и многие другие. Кроме того, графические модели позволяют проверить правильность решения задачи, их можно использовать для проведения исследования, так как они помогают выявить условия, при которых задача имеет (или не имеет) решения, найти число решений, выявить, как изменяется значение искомой величины в зависимости от изменения данных величин, и т.д.