Сравнение методов и алгоритмов обработки и анализа изображений

Аннотация. В данной статье проводится сравнение метода BRISK, который используются для нахождения особых точек на изображении. Так же для проверки эффективности данного метода было произведено сравнение с методами FAST, SURF, ORB.Сравнение производилось в среде MATLAB.

Методы поиска особых точек являются важной технологией обработки изображений и широко применяется для медицины, распознавания образов, дистанционного зондирования и компьютерного зрения.

Экспериментальные исследования

Целью экспериментальных исследований являлся сравнение метода BRISK с методами SURF, FAST, ORB. Сравниваться эти методы будут по быстродействию, устойчивости к повороту, смещению, среднеквадратическому отклонению.

Что бы узнать устойчивы методы к повороту или смещению, мы исследуем изменения элементов матрицы геометрических преобразований, которая формируется при сопоставлении точек двух изображений. Матрица размерностью 3х2  имеет вид:

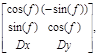                                                                                                            (3)

где  f - угол поворота изображения вокруг начальной точки, Dx, Dy- смещение по соответствующим осям.

Среднеквадратическая отклонение - дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом S.

Среднеквадратическое отклонение находится по формуле:

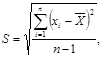                                                                                                               (4)

где 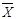- среднее арифметическое значение результатов n измерений, который вычисляется по формуле:

                                                                                                                 (5)

где - сумма результатов измерения, а n- число измерений.

Построим график зависимости ошибки угла поворота при методах BRISK, SURF, FAST, ORB представленном на рисунке 1 и рассчитаем среднеквадратическое отклонение (Таблица 1).

Таблица 1.

Среднеквадратическое отклонение при повороте изображения

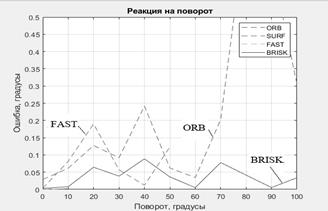
Рисунок 1. Ошибка оценки поворота

Далее исследуем реакцию алгоритмов на смещение двух изображений. График реакции двух методов изображён на рисунке 18 с шагом 20 пикселей. Среднеквадратическое отклонение методов показана в таблице 2.

Таблица 2.

Среднеквадратическое отклонение при смещении изображения

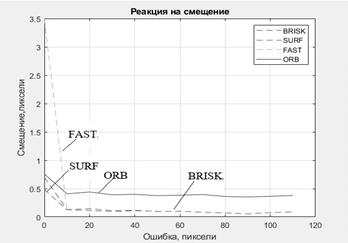
Рисунок 2. Ошибка оценки при смещении

Далее проведем исследование быстродействия данных методов. Замерим время выполнения этих двух методов при смещении. Результаты показаны на рисунке 3.

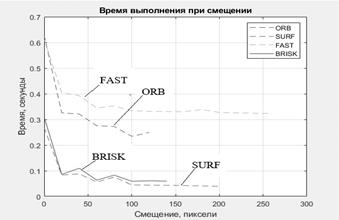
Рисунок 3. Время выполнения алгоритмов при смещении

Таким образом, по графикам можно понять, что все методы инвариантны к сдвигу и повороту изображения, что говорит о том что их можно использовать при различный геометрических преобразованиях, таких как смещение или поворот. Но при этом среднеквадратическая ошибка BRISK меньше, а быстродействие больше чем у других методов, что говорит о его большей эффективности при обработке изображений.