РАСЧЁТ СЛОЖНЫХ ЦЕПЕЙ С ПРИМЕНЕНИЕМ ПРИНЦИПА НАЛОЖЕНИЯ ТОКА

Электрическая цепь — это система, состоящая из источников электрической энергии, потребителей и проводников, которые соединяют все элементы в замкнутый контур. Такой контур обеспечивает непрерывное движение электрического тока, позволяя выполнять полезную работу.

Принцип наложения токов (принцип суперпозиции) утверждает, что в линейной электрической цепи с несколькими источниками напряжения ток в любом элементе равен сумме токов, которые возникают от каждого источника по отдельности, при условии, что все остальные источники заменены их внутренними сопротивлениями. Мне дана задача и схема, в которой необходимо найти результирующие токи на каждом из резисторов. При условии, что Е₁=50 В, Е₂=80 В, Е₃=30 В, и R₁=800 Ом, R₂=24 Ом, R₃=630 Ом.

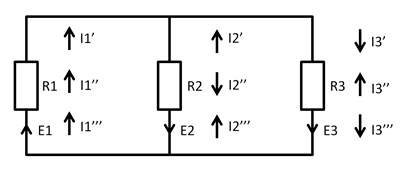
Рисунок 1. Схема

Решение:

Рассмотрим задачу, чтобы на её решить надо использовать принцип наложения токов. Для нахождения сил токов мне надо выяснить направления их суммируемых токов, их будет 3, так как нам дано 3 ЭДС. Смотрим по каждому из ЭДС: Е₁ направлено через первый резистор и идёт разветвляясь на резисторы R₂ и R₃;  Е₂ сразу разветвляется и идёт на резисторы R₁ и R₃, после соединяется в R₂; Е₃ так же разделяется, но идя на R₁ и R₂, потом в R₃. Направления найдены, можно приступать к решению.

При Е₁:

Для начала нам следует найти общую силу тока которая сразу даст одну из суммирующихся сил при данном ЭДС(последовательное соединение проводников), чтобы её найти мне необходимо знать общее сопротивление. При любом ЭДС в данной схеме R_общ будет находиться через формулу и параллельного и последовательного соединения.

R_общ=(R₂*R₃)/(R₂+R₃)+R₁=(24*630)/(24+630)+800=823,12 Ом

I_общ=I₁’=E₁/ R_общ=50/823,12=0,061 А

Теперь отдельно рассматриваем узел с R₂ и R₃. I₂₃= I_общ, так как соединение последовательное. Значения сопротивлений нам даны, а значение напряжения на данном участке будет равно для каждого резистора, так как тут уже параллельное соединение.

R₂₃=(R₂*R₃)/(R₂+R₃) =(24*630)/(24+630)=23,12 Ом

U₂₃= I_общ* R₂₃=0,061*23,12=1,41 В

Нам уже известны все данные чтобы найти остальные силы тока с данной ЭДС:

I₂’= U₂₃/ R₂=1,41/24=0,06 А

I₃’= U₂₃/ R₃=1,41/630=0,0022 А

Таким же методом находим другие силы тока на остальных ЭДС

При Е₂:

R_общ=(R₁*R₃)/(R₁+R₃)+R₂=(800*630)/(800+630)+24=376,45 Ом

I_общ=I₂’’=E₂/ R_общ=80/376,45=0,21 А

R₁₃=(R₁*R₃)/(R₁+R₃) =(800*630)/(800+630)=352,45 Ом

U₁₃= I_общ* R₁₃=0,21*352,45=74,0145 В

I₁’’= U₁₃/ R₁=74,0145/800=0,0925 А

I₃’’= U₁₃/ R₃=74,0145/630=0,1175 А

При Е₃:

R_общ=(R₁*R₂)/(R₁+R₂)+R₃=(800*24)/(800+24)+630=653,3 Ом

I_общ=I₃’’’=E₃/ R_общ=30/653,3=0,046 А

R₁₂=(R₁*R₂)/(R₁+R₂) =(800*24)/(800+24)=23,3 Ом

U₁₂= I_общ* R₁₂=0,046*23,3=1,07 В

I₁’’’= U₁₂/ R₁=1,07/800= А

I₂’’’= U₁₂/ R₂=1,07/24= А

И так, теперь нам известны все токи, по направлению либо складываем, либо вычитаем и получаем I₁, I₂, I₃.

I₁=I₁’+I₁’’+I₁’’’=0,61+0,0925+0,0013=0,1548 А

I₂=I₂’+I₂’’-I₂’’’=0,06+0,21-0,045=0,225 А

I₃=-I₃’+I₃’’-I₃’’’=-0,0022+0,1175-0,046=0,0693 А

В ходе работы был успешно применён метод наложения для расчёта сложной электрической цепи с тремя источниками ЭДС. Получены значения результирующих токов: I₁=0,1548 А, I₂=0,225 А, I₃=0,0693 А

Проведённый расчёт наглядно продемонстрировал основные преимущества принципа суперпозиции:

1. Сведение сложной задачи к серии простых. Расчёт цепи с несколькими источниками заменяется расчётом нескольких цепей с одним источником, что значительно упрощает анализ.
2. Наглядность и методическая ценность. Метод позволяет чётко проследить вклад каждого источника энергии в формирование токов в цепи.

Несмотря на свою эффективность для линейных цепей, метод может быть достаточно трудоёмким при большом количестве источников. Тем не менее, его освоение является обязательным для инженеров-электротехников, так как он закладывает основу для понимания более сложных методов анализа и моделирования электрических цепей. Полученные навыки могут быть использованы для проектирования, диагностики и оптимизации работы реального электрооборудования.