Разработка модели фильтра Калмана для системы управления беспилотным летательным аппаратом

Среди объектов исследований, наиболее подверженных воздействию различного рода помех, самыми распространенными являются системы навигации. Одним из методов, способствующих улучшению качества работы таких объектов, является применение алгоритмов фильтрации сигналов измерительных приборов, оценки параметров движения, в частности, фильтра Калмана [2, c. 47]. 

В данной статье будет рассмотрен процесс разработки математической модели движения беспилотного летательного аппарата (БПЛА), синтез фильтра Калмана и его реализация в виде программного кода в среде MATLAB.

На рисунке 1 изображена обобщенная структурная схема модели САУ БПЛА.

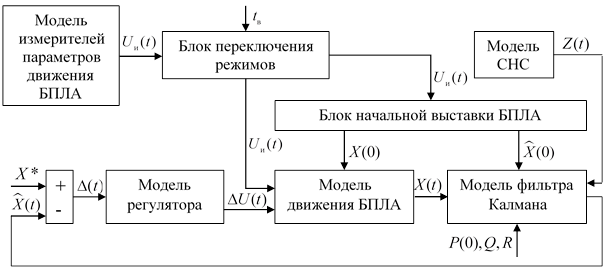
Рисунок 1. Структурная схема модели САУ БПЛА

Для разработки модели движения БПЛА возьмем следующие исходные данные для построения модели движения и синтеза фильтра Калмана:

Тангаж ϑ = 0^о;

Крен γ = 0^о;

Курс ψ = 5^о;

Начальные скорости движения W_N = 18 м/с, W_E = 0 м/с;

Среднеквадратическое отклонение (СКО) шума измерителя угловой скорости σ_ω = 10^-5 рад/с;

СКО шума измерителя ускорения σ_a = 10^-2 м/с²;

СКО шума СНС (спутниковой навигационной системы) σ_снс = 0,2 м/с.

Значение γ и W_{E_СНС} принять равными 0.

Для написания программного кода в среде MATLAB [1, c. 36], необходимо в главном меню выбрать вкладку File→New → Script.

После компиляции программного кода, реализующего модель движения БПЛА и фильтра Калмана, были посчитаны матрицы массивов (рис. 2).

Рисунок 2. Матрицы массивов движения БПЛА и фильтра Калмана

Результаты моделирования, отражающие динамику тангажа, крена, курса, северной и восточной составляющих скоростей движения БПЛА, показаны на рисунках 3 – 7 соответственно.

Рисунок 3. Динамика тангажа БПЛА

Рисунок 4. Динамика крена БПЛА

Рисунок 5. Динамика курса БПЛА

Рисунок 6. Динамика северной составляющей скорости БПЛА

Рисунок 7. Динамика восточной составляющей скорости БПЛА

Из анализа графиков можно сделать выводы, что углы ориентации, вычисленные из модели динамики БПЛА, отклоняются от заданных значений на большую величину, в то время как оценки фильтром Калмана указанных координат состояния намного точнее и практически не уходят от истинных показаний. То же самое можно сказать и о скоростях движения. Их оценки фильтром Калмана намного меньше, чем максимальное значение шума измерений СНС.