Теория сделок абсолютного позиционного спекулянта-любителя единственной корпорации

Данная статья не является некой непоколебимой инструкцией по осуществлению торговли на рынке ценных бумаг, но определяет некоторый показатель, имеющий способность дать приблизительный ответ на вопрос: «Покупать акции данной корпорации или продавать в первоначальный момент открытия торговли и именно этой или другой в сравнении?».

В настоящее время молодежь после поступления в высшее учебное заведение начинает интересоваться возможностью обзавестись пассивным доходом, а точнее в среднем 58% студентов [1, c. 45]. Большая часть этих студентов не рассматривает явление акционером как нечто, приносящее прибыль, считая это чем-то, стоящим выше их способностей, либо недоступной альтернативой тому, что они в итоге выбирают [2, c. 220].

Однако 10% всех студентов считают спекуляцию на фондовом рынке жизнеспособной в границах пассивного дохода учащегося, но лишь 1% всё-таки начинает реально действовать в этом направлении. Половина из последних в итоге падает в «яму» бинарных опционов, но эта статья не затрагивает рассмотрение данного явления. Для оставшихся же является всегда злободневной проблема правильного выбора корпораций для работы с их акциями в условиях постоянной учёбы и явной зависимости от свободного времени для торговли ценными бумагами.

На рисунке 1 представлена круговая диаграмма для наглядности проведенного социального опроса с применением выборки.

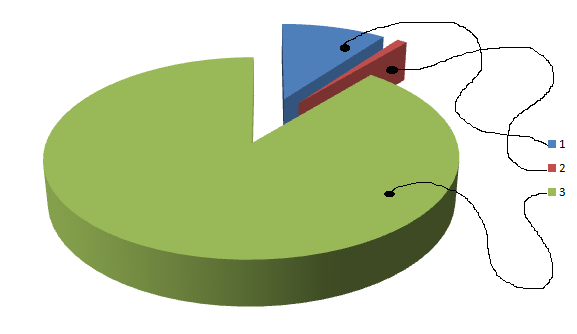
Рисунок 1. Круговая диаграмма: 1 – полагают спекуляцию возможной; 2 – реально совершают сделки на фондовом рынке; 3 – прочие

Основная часть настоящей статьи раскрывает частичный («один из …») ответ на вопросы вторых: на какое открытое акционерное общество обратить внимание в условиях студенческой занятости и играть на повышение или спад.

Явного ответа статья не даёт, она на это и не рассчитана, но пытается раскрыть «путь» отыскания.

Искусственный ввод понятийных операндов:

Единственная корпорация – открытое акционерное общество, совокупно удовлетворяющее все потребности своего миноритария в смысле его абстрагирования от желания явиться акционером другой компании.

Абсолютный позиционный спекулянт-любитель – это такой позиционный спекулянт-любитель, чьи нужды удовлетворяются единственной корпорацией.

Отныне все предполагаемые действия совершаются от лица абсолютного позиционного спекулянта-любителя, и все следствия из них трактуются его моделями.

Введём условные обозначения для чёткой установки формул сравнения корпораций и типа грядущих сделок:

 – планируемое время торговли в днях;

 – количество сделок в день (частота);

 – анализируемый прошедший промежуток времени:

оптимальное значение ;

 – максимальная цена ценной бумаги за ;

 – максимальная цена ценной бумаги за ;

 – средняя разность экстремумов цен;

 – верхняя цена второго уровня;

 – верхняя цена третьего уровня;

 – нижняя цена второго уровня;

 – нижняя цена третьего уровня;

 – число пересечений -ой цены -ого уровня за , где

 = {верхняя, нижняя},  = {2; 3}.

Теперь введём апостериорные функции верхней и нижней цен соответственно:

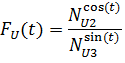
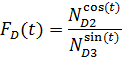
Далее предлагаются формулы абсолютных интегральных показателей верхней и нижней цен соответственно:

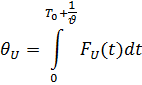
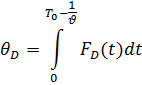
Помимо этого предлагаются формулы характеристических поверхностей:

Характеристические поверхности при выборе типа сделки и единственной корпорации не применяются, в данном смысле не несут нагрузку. В вышеописанном выборе помогает абсолютный полный интегральный показатель: 

Если абсолютный полный интегральный показатель отрицателен, то в приоритете продажа ценных бумаг, иначе – покупка. При нулевом показателе не рекомендуется действовать. Для сравнения корпораций на предмет именования единственной применяется модуль абсолютного полного интегрального показателя: чем больше его значение, тем выше степень её «единственности».

Вычислим на примере значения функций верхней и нижней цен, абсолютных интегральных показателей, а также построим характеристические поверхности:

Пусть 

Тогда 

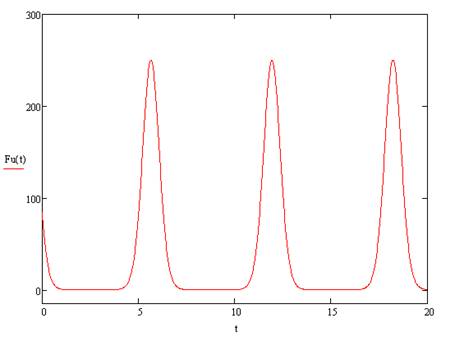
Рисунок 2. График функции верхней цены

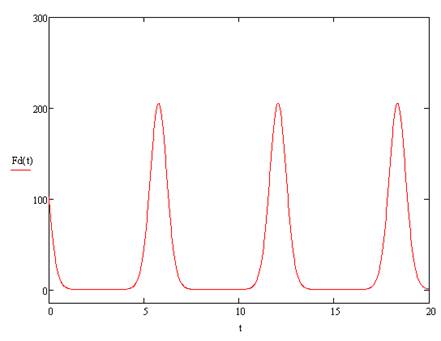
Рисунок 3. График функции нижней цены

Вычислив, имеем: , а , тогда  Сравнение корпораций производится после аналогичного вычисления показателей акций второй компании. В этой статье такого примера не приводится.

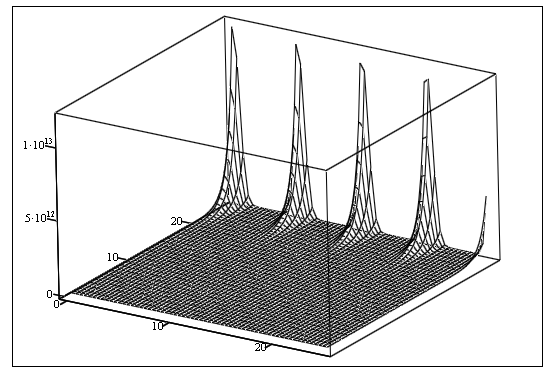
Рисунок 4. Характеристическая поверхность 

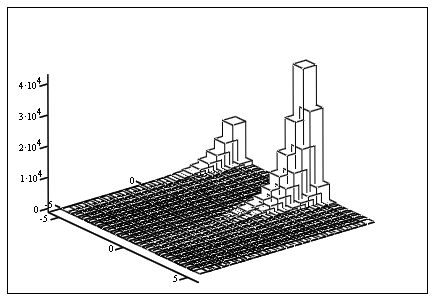
Рисунок 5. Характеристическая поверхность