Повышение несущей способности цельнодеревянных балок с установкой стержневой арматуры
Секция: Технические науки

XL Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Повышение несущей способности цельнодеревянных балок с установкой стержневой арматуры
Строительство считается главным потребителем материалов из древесины в промышленной индустрии, вследствие чего подымаются закономерные вопросы: сохранение лесных ресурсов, рациональное внедрение материалов, уменьшение себестоимости материалов и дел, увеличение эксплуатационных данных строй систем. В данной связи животрепещуще увеличение несущей возможности древесных систем при сохранении геометрических объемов поперечного сечения составляющих, а еще создание свежих действенных систем при одновременном понижении материалоемкости и усовершенствовании технико-экономических характеристик [1].
Армирование считается одним из действенных методик увеличения несущей возможности древесных систем[2], которое понижает воздействие влияния недостатков и пороков деревянных конструкция на крепкость и преждевременное разрушение систем.
Необходимой практической задачей считается разработка инженерного способа расчета армированных древесных балок, предусматривающего разнородность и долгие механические свойства древесной породы, действующие на надежность и долговечность систем.
Классический метод расчета строительных конструкций базируется на основных положениях теории упругости, и поэтому, расчет деревянных конструкций производится с позиции упругой работы древесины. Одновременно с этим поперечный изгиб сопровождается значительными эффектами нелинейности, большими прогибами и сопровождается перераспределением напряжений по сечению изгибаемого элемента на разных этапах загружения балок рис. 1.
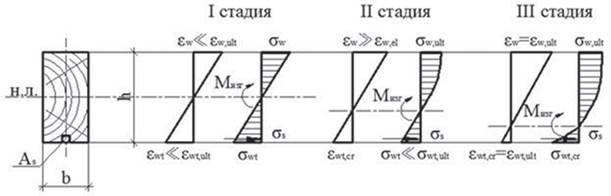
Рисунок 1. Стадии напряженно-деформированного состояния армированной деревянной балки
В начальной стадии древесина работает упруго, деформации намного меньше предельных значений (ɛw << ɛw,ult; ɛw,t << ɛwt,ult), эпюры деформаций и напряжений имеют линейный характер. На второй стадии эпюра напряжений становится криволинейной, и нейтральная линия смещается в сторону растянутой кромки. Арматура начинает воспринимать растягивающие усилия σs , а напряжения в растянутой зоне древесины все еще меньше предельного значения (σw,t << σwt,ult ). На этом этапе работы элемента начинается смятие в крайних волокнах сжатой зоны, где появляются характерные складки (ɛw << ɛw,el). На последней стадии (стадии разрушения) зона пластичности развивается вглубь сечения, нейтральная линия еще больше смещается к растянутой кромке. Деформации древесины в обеих зонах достигают своих предельных значений (ɛw = ɛw,ult; ɛw,t = ɛwt,ult), а напряжения в древесине растянутой зоны доходят до своего критического значения σwt,cr. Разрушение происходит от разрыва крайних растянутых волокон древесины часто при неполном использовании прочности растянутой арматуры.
В различных источниках представлена методика расчета армированных клееных деревянных балок, где в основу также положена первая стадия напряженно-деформированного состояния. В этом случае считается, что связь между древесиной и арматурой непрерывна по всей длине балки и обеспечивает надежность их полной совместной работы на протяжении всего срока эксплуатации [3, 4].
Одним из ключевых моментов в расчете армированных деревянных конструкций является необходимость учета перераспределения усилий между древесиной и арматурой. Однако существующие методы не позволяют оценить напряжения в арматуре и оптимально подобрать ее прочностные и деформационные характеристики.
На работу изогнутого элемента оказывают существенное влияние пороки древесины. Влияние пороков на сопротивление изгибу элементов деревянных конструкций учитывается введением коэффициента однородности ⱪодн = 0,4 [5].
Влияние длительности действия нагрузки на элемент деревянной конструкции учитывается введением коэффициента длительности сопротивления древесины. Коэффициент длительности определяют экспериментально по результатам испытания образцов древесины на длительное действие постоянной нагрузки. Коэффициент длительности определяют отношением предела длительного сопротивления к пределу кратковременного сопротивления. Эта величина зависит от породы древесины и других факторов и составляет по разным источникам ⱪдл = 0,5÷0,8 [6-9].
До разработки инженерного метода расчета усиления цельнодеревянных балок стержневой арматурой в растянутой зоне предварительно выполнен численный эксперимент в универсальной программной системе конечно-элементного анализа ANSYS.
В исходных данных к расчету была принята цельнодеревянная балка из древесины сосны, усиленная по всей длине растянутой зоны арматурой периодического профиля из стали. Размеры балки 50х100х2000 мм. Расчетное сопротивление древесины на изгиб 14 МПа, модуль упругости 10 ГПа. Диаметр арматуры 8 мм. Расчетное сопротивление арматуры растяжению 390 МПа, модуль упругости растяжения 200 ГПа.
Общий вид поперечного сечения усиленной балки представлен на рис. 2.
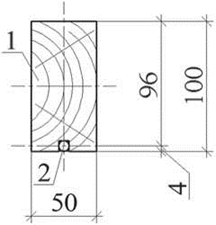
Рисунок 2. Разрез армированной цельнодеревянной балки: 1 — цельнодеревянный брус; 2 — арматурный стержень
Результаты численного моделирования цельнодеревянной балки с одиночным армированием в растянутой зоне в программной системе ANSYS представлены на Рис. 3-6.
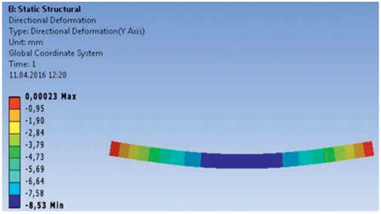
Рисунок 3. Общие деформации балки
Из Рис. 3 видно, что максимальный прогиб балки составляет 8,53 мм.
На Рис. 4 максимальные напряжения растяжения в крайних волокнах составляют 14,02 Мпа, а максимальные напряжения сжатия составляют 10,45 МПа.

Рисунок 4. Распределение нормальных напряжений в поперечном сечении балки в середине пролета
На Рис. 5 представлено распределение нормальных напряжений в арматурном стержне. Среднее растягивающее напряжение в арматуре составляет 192,80 МПа.
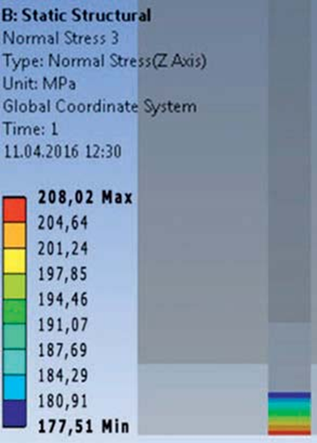
Рисунок 5. Распределение нормальных напряжений в растянутой арматуре
Из Рис. 6 видно, что положению нейтральной линии соответствует значение 57,43 мм, считая от сжатой кромки балки.
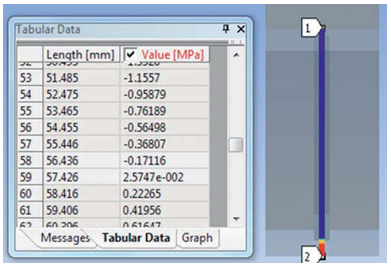
Рисунок 6. Положение нейтральной линии
После получения результатов в программном комплексе ANSYS была поставлена задача разработать инженерный метод расчета деревянных балок, усиленных стержневой арматурой в растянутой зоне.
Предлагается следующий метод инженерного расчета усиления деревянных балок стержневой арматурой в растянутой зоне.
1. Напишем уравнение равновесия внутренних усилий в поперечном сечении балки на ось x Рис. 7:
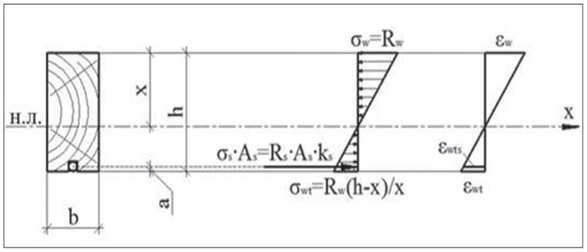
Рисунок 7. Схема к определению высоты сжатой зоны
![]() , (1)
, (1)
где ![]() -напряжения в древесине сжатой зоны, кг/см2;
-напряжения в древесине сжатой зоны, кг/см2;
![]() -высота сжатой зоны древесины, см;
-высота сжатой зоны древесины, см;
![]() -напряжения в древесине растянутой зоны, кг/см2;
-напряжения в древесине растянутой зоны, кг/см2;
![]() -высота поперечного сечения деревянной балки, см;
-высота поперечного сечения деревянной балки, см;
![]() -напряжения в растянутой арматуре, кг/см2;
-напряжения в растянутой арматуре, кг/см2;
![]() -площадь поперечного сечения арматуры, см2.
-площадь поперечного сечения арматуры, см2.
2. В формуле (1) выразим ![]() через
через ![]() и
и ![]() , тогда:
, тогда:
![]() , (2)
, (2)
![]() . (3)
. (3)
3. Учитывая, что при усилении растянутой зоны высота сжатой зоны ![]() всегда больше
всегда больше ![]() , напряжения сжатия в древесине
, напряжения сжатия в древесине ![]() в предельном состоянии достигнут своего расчетного сопротивления
в предельном состоянии достигнут своего расчетного сопротивления ![]() , в то время как напряжения растяжения в древесине
, в то время как напряжения растяжения в древесине ![]() будут меньше расчетного сопротивления
будут меньше расчетного сопротивления ![]() .
.
4. В предельном состоянии получим значения напряжений в сжатой и растянутой зонах поперечного сечения балки:
![]() , (4)
, (4)
![]() . (5)
. (5)
5. Выразим высоту сжатой зоны древесины ![]() из условия (1):
из условия (1):
![]() (6)
(6)
где ![]() -ширина поперечного сечения балки, см;
-ширина поперечного сечения балки, см;
![]() -модуль упругости древесины, кг/см2;
-модуль упругости древесины, кг/см2;
![]() -расстояние от центральной оси стержня растянутой арматуры до кромки растянутой зоны, см.
-расстояние от центральной оси стержня растянутой арматуры до кромки растянутой зоны, см.
6. Одновременно с этим растянутая арматура ввиду своих жесткостных характеристик и положения по высоте сечения элемента может быть не полностью загружена по критерию прочности и не достигать напряжений текучести. Для этого из условия равенства относительных деформаций в месте положения арматуры определим коэффициент использования несущей способности растянутой арматуры в предельном состоянии при условии наличия совместной работы древесины и элемента усиления на Рис. 7:
![]() , (7)
, (7)
![]() . (8)
. (8)
где ![]() -относительная деформация растянутой древесины в месте расположения арматуры;
-относительная деформация растянутой древесины в месте расположения арматуры;
![]() -фактическая относительная деформация арматуры;
-фактическая относительная деформация арматуры;
![]() -предельная относительная деформация растянутой арматуры;
-предельная относительная деформация растянутой арматуры;
![]() -расчетное сопротивление арматуры растяжению, кг/см2;
-расчетное сопротивление арматуры растяжению, кг/см2;
![]() -модуль упругости арматурной стали в растянутой зоне, кг/см2.
-модуль упругости арматурной стали в растянутой зоне, кг/см2.
7. Из пропорции для относительных деформаций материала в поперечном сечении балки получим:
![]() , (9)
, (9)
![]() . (10)
. (10)
8. Коэффициент использования несущей способности растянутой арматуры находим из отношения существующих относительных деформаций древесины в месте расположения арматуры ![]() и предельно возможных относительных деформаций арматуры
и предельно возможных относительных деформаций арматуры ![]() :
:
![]() , (11)
, (11)
![]() . (12)
. (12)
Запишем коэффициент использования растянутой арматуры ![]() через механические характеристики материала при
через механические характеристики материала при ![]() и
и ![]()
![]() , (13)
, (13)
При этом должно выполняться условие, что коэффициент ![]() должен быть меньше 1. В случаях, когда коэффициент превышает ограничение, значение коэффициента принимается равным 1, потому как в противном случае это будет означать, что арматура несет больше своего расчетного сопротивления. Значения коэффициента различаются в зависимости от модуля упругости применяемой арматуры и ее положения по высоте сечения.
должен быть меньше 1. В случаях, когда коэффициент превышает ограничение, значение коэффициента принимается равным 1, потому как в противном случае это будет означать, что арматура несет больше своего расчетного сопротивления. Значения коэффициента различаются в зависимости от модуля упругости применяемой арматуры и ее положения по высоте сечения.
9. Продольное усилие в арматурном стержне находится по формуле:
![]() (14)
(14)
10. Максимальный изгибающий момент, который сможет вынести балка, складывается из изгибающих моментов, возникающих в основном материале конструкции и элементе усиления от действия внешней нагрузки относительно нейтральной линии.
11. Изгибающий момент от равнодействующей нормальных напряжений в древесине сжатой зоны определяется по формуле:
![]() . (15)
. (15)
12. Изгибающий момент от равнодействующей нормальных напряжений в древесине растянутой зоны определяется по формуле: продольные усилия в стержневой арматуре, что очень важно для оптимального подбора прочностных и деформационных свойств элементов усиления и более полного их вовлечения в работу.
![]() . (16)
. (16)
Заменив в формуле (16) ![]() через
через ![]() получим:
получим:
![]() . (17)
. (17)
13. Изгибающий момент от продольного усилия, возникающего в арматурном стержне, вычисляется по формуле:
![]() (18)
(18)
![]() (19)
(19)
14. Когда сложив моменты в формулах (15), (17) и (19), получим формулу для определения несущей способности балки:
![]() (20)
(20)
![]() (21)
(21)
Исходя из данной методике, выполнен инженерный расчет цельнодеревянной балки, армированной в растянутой зоне стальным стержнем.
Результаты инженерного расчета по предложенному алгаритму и численного моделирования в программной системе ANSYS представлены в табл. 1.
Таблица 1.
Результаты расчетов цельнодеревянной балки, армированной в растянутой зоне стержневой арматурой
|
Параметры, определяемые в расчете |
Расчет в ANSYS |
Инженерный метод расчета |
Погрешность, % |
|
Напряжения в древесине, МПа: -сжатие -растяжение |
14,03 10,46 |
14,00 10,33 |
0,21 1,26 |
|
Напряжения в арматуре, МПа |
187,31 |
187,17 |
0,07 |
|
Усилие в арматуре, кН |
9,18 |
9,17 |
0,11 |
|
Положение нулевой линии, мм |
57,43 |
57,54 |
0,19 |
Заключение
По полученным результатам численного эксперимента в программной системе ANSYS и инженерного метода расчета выявлено практически полное совпадение результатов с незначительными погрешностями до 1,3%.
Предложенный инженерный метод расчета армированных стержневой арматурой в растянутой зоне балок из древесины дает хорошие результаты и может с высокой степенью достоверности применяться для расчета несущей способности цельнодеревянных балок, усиленных стержневой арматурой в растянутой зоне.
Помимо этого, в отличие от других методов расчета, новая методика позволяет дополнительно определять продольные усилия в стержневой арматуре, что очень важно для оптимального подбора прочностных и деформационных свойств элементов усиления и более полного их вовлечения в работу.
Целью дальнейшей научно-исследовательской работы являются экспериментальные исследования работы балок из древесины, армированные стальной арматурой по всей длине растянутой зоны.





