Исследование функции Аккермана

Введение

В наше время известно большое количество интересных функций. Одной из них является функция Аккермана. Удивительная по своим свойствам и возможностям функция. Она является простым примером всюду определенной вычислимой функции, которая не является примитивно рекурсивной. Ее аргументами являются два неотрицательных целых числа, а возвращаемым значением является натуральное число. Обозначение:

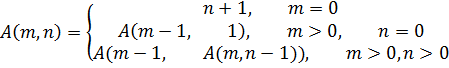
Одним из отличительных особенностей этой функции является то, что она растет очень быстро. К примеру, уже при  и  ее значение .

На практике можно часто встретить обратную функцию Аккермана, которую используют для исследования сложности различных алгоритмов, так как в отличие от обычной функции – обратная растет очень медленно.

Исследование

Нам стало интересно посмотреть, что скрывает в себе эта таинственная функция, какие ее особенности еще можно обнаружить. Поэтому нами был произведен ряд расчетов с помощью программы, написанной на языке С.

Ниже представлена таблица значений, полученная с помощью программы (см. Приложение 1) и аналитического вывода значения.

Примечание: для получения некоторых значений нам пришлось использовать итерационный вариант функции Аккермана (см. Приложение 2).

Таблица 1.

Значения функции Аккермана

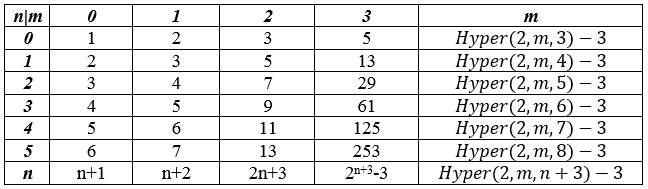
Примечание:  – гипероператор, который является обобщением арифметических операций сложения, умножения и возведения в степень, рассматриваемых как гипероператоры 1-го, 2-го и 3-го порядка соответственно, на высшие порядки.

Гипероператор порядка  с аргументами  и  обозначается a⁽ⁿ⁾ (b) и рекурсивно определяется как результат многократного применения гиперопретора порядка  к последовательности из  одинаковых аргументов, каждый из которых равен.

·        сложение  и  — увеличение числа a на количество единиц, равное b:

{\displaystyle a{^{(1)}}b=a+\underbrace {1+1+\dots +1} _{b}=a+b}

·        умножение  на  — сложение числа  с самим собой раз:

·        возведение a в степень b — умножение числа a на само себя b раз:

·         

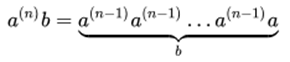
В последнем выражении операции выполняются справа налево, что является существенным, так как гипероператоры порядка  не являются ни коммутативными, ни ассоциативными. Гипероператоры 4-го, 5-го и 6-го порядка называются «тетрация», «пентация» и «гексация» соответственно.

Общая рекурсивная формула имеет следующий вид:

Данная формула описана в Приложении 4.

Были построены следующие графики для исследования данной функции:

Рисунок 1. Функция Аккермана при фиксированных значениях m

Рисунок 2. Функция Аккермана при фиксированных значениях n

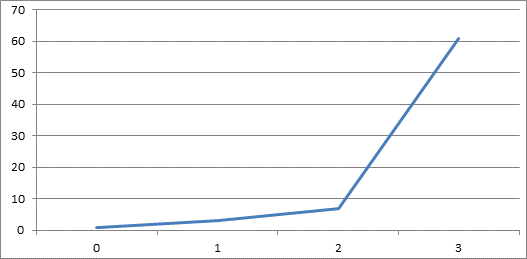
Рисунок 3. Функция Аккермана при m=n

Отсюда можно сделать предположение, что данная функция имеет большой скачок, начиная со значений  и .

Одним из свойств примитивно рекурсивных функций является то, что они не могут быстро расти. Значит можно попробовать показать, что функция Аккермана не является примитивно рекурсивной.

Попробуем доказать теперь это.

Прежде всего отметим, что мы ограничиваем функцию g следующим образом:

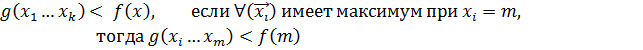
Для унарных функций неравенство будет выполняться для каждого входного значения, так что  во всех точках.

Теперь, имея это в виду, мы попробуем доказать, что функция Аккермана не является примитивной рекурсивной, так как все примитивно-рекурсивные функции можно ограничить сверху функцией Аккермана.

Произведем некоторые вычисления

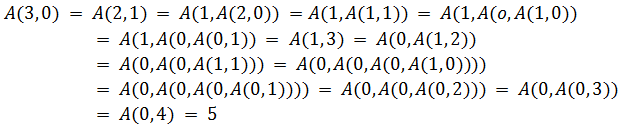
Отсюда видно, что сложность расчета быстро возрастает по мере продвижения по функциональному пространству. Для примера возьмем  значение . Таким образом, хотя и существует метод, который приведет к результату функции Аккермана, но вычисление точного значения занимает достаточно долгое время.

В частности, мы покажем, что:

, где PR - множество примитивно-рекурсивных функций.

Доказательство:

Необходимо доказать пять случаев, первые три из которых тривиальны.

Аналогично, преемническая функция  не увеличивается с той же скоростью, что и функция Аккермана, поэтому нам нужно только проверить возможности, что (I) состав примитивно-рекурсивных функций или (II) рекурсивная конкатенация (*) примитивно рекурсивных функций "увеличивается с большей скоростью", чем функция Аккермана. Покажем, что такая функция не существует и, следовательно, функция Аккермана не является примитивно-рекурсивной функцией.

(*): Конкатенация – бинарная операция, определенная на словах данного алфавита.

Обозначения:

·        A – алфавит

·         – слова из букв алфавита

·        a₁…a_n и b₁…b_n – записанные подряд буквы слова

Если , то

Теперь докажем (I):

Допустим , где f, g, h –примитивно рекурсивные функции.

так, что , где  являются первыми параметрами функции Аккермана. Затем допустим, что , тогда мы должны показать, что:

Распишем композицию функции Аккермана:

                                                          x раз

Теперь покажем еще две вещи, которые помогут в доказательстве. Можно заметить, что:

1.                                                                                                     (1)

2.                                                                                         (2)

Мы можем показать, что (1) следует из того, что . Теперь распишем для :  Так как при увеличении m будет расти значение композиции функции Аккерамана, то (1) выполняется.

Рассмотрим (2) и распишем функцию Аккермана:

     x раз

Это завершает доказательство (2), так как простой случай, когда число композиций Аккермана равно 0, то есть

Вспоминая наши начальные неравенства: , где   – примитивно рекурсивная функция.

Теперь можно заметить, что: , но

Отсюда можно заметить:

Этим завершаем доказательство (I), так как существует значение функции Аккермана, которое строго больше композиции любых двух примитивно рекурсивных функций, имеющих одинаковые входные значения.

Остается доказать (II):

Для этого предположим, что существует функция  определяемая рекуррентными уравнениями.

Тогда, поскольку  примитивно рекурсивна мы знаем, что существует функция Аккермана , которая больше чем , и мы можем показать, что  для некоторого m > 0.

По методу математической индукции:

Базовый случай: мы знаем, что  является постоянной функцией, являющейся примитивно-рекурсивной унарной проекционной функцией, поэтому по более ранним наблюдениям существует функция Аккермана,  больше  , Это завершает базовый случай.

Индукционная гипотеза: Предположим, что наблюдение выполняется для всех случаев .

Пусть , а

Тогда:

Так как g возрастает. По предположению индукции мы знаем:

Отсюда подстановкой и нашим выбором для  имеем:

Отсюда мы знаем по определению функции Аккермана и подстановки, что:

Теперь мы можем сказать, что , откуда следует что функция Аккермана не является примитивно рекурсивной, так как она больше всех примитивно рекурсивных функций.

Далее рассмотрим обратную функцию Аккермана.

Таблица 2.

Значения обратной функции Аккермана

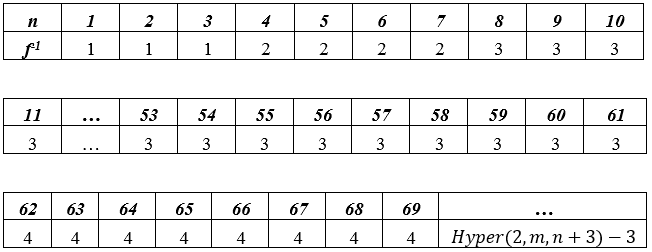
Рисунок 4. Обратная функция Аккермана

Отсюда мы можем заметить, что практически для всех чисел, встречающихся при работе с различными алгоритмами, значение обратной функции Аккермана будет меньше 5.

Также интересно рассмотреть количество рекурсивных вызовов функции Аккермана для тех или иных аргументов. Например, для вычисления  необходимо вычислить предварительно . Тогда имеем пять вызовов функции Аккермана.

Написав соответствующую программу получили следующие результаты

Таблица 3.

Результаты

Сравнивая графики и таблицы значений функции Аккермана и количества рекурсивных вызовов для соответствующих аргументов, можно предположить, что данная функция растет быстрее функции Аккермана.

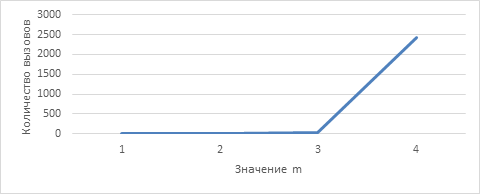
Рисунок 5. Количество рекурсивных вызовов функции A(m,m)

Чтобы получить такую функцию необходимо, чтобы наша новая функция выполняла аналогичное функции Аккермана рекурсивное погружение, но на каждом шаге увеличивала своё значение на единицу, а при выполнении условия прекращения рекурсии, , возвращала не , а , так как в данном случае функция вызвана один раз. Для условия  функция аналогична функции Аккермана но к значению прибавляется единица, то есть к количеству вызовов функции  добавляется еще и тот вызов, который совершается сейчас. Для последнего условия понадобится использовать значение  для того чтобы рекурсия пошла по такому же пути как и у функции Аккермана, но к этому значению необходимо прибавить , чтобы учесть количество рекурсивных вызовов , и также не забыть прибавить единицу, соответствующую актуальному вызову. В итоге получаем функцию, рекурсивные вызовы которой абсолютно симметричны функции Аккермана, а отличается лишь возвращаемыми значениями, соответствующими количеству рекурсивных вызовов. Тогда получаем следующую функцию:

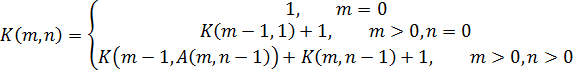
Сперва поговорим об одном интересном наблюдении, а затем вернёмся к вопросу о росте функции. Если мы введем функцию

Причём, чтобы получить такую функцию, необходима функция выполняющая аналогичное  рекурсивное погружение, и увеличивающая возвращаемое значение на единицу на каждом шаге рекурсии, а при выполнении условия прекращения рекурсии возвращающая 1. Так как функция  выполняет погружение аналогичное функции Аккермана, то мы имеем те же вводные, что и для вывода функции, то есть задача сводится к уже решенной, что свидетельствует о тождественном равенстве функции

Получаем что , то есть количество рекурсивных вызовов функции  при вычислении её значения будет равно её собственному значению.

Вернемся к вопросу о степени роста функции. Обратив внимание на вид функции Аккермана можно увидеть, что возвращаемое значение будет равно аргументу n увеличенному на единицу от последнего рекурсивного вызова. Чтобы понять какая функция быстрее растет проследим за изменениями n на протяжении всей цепочки вызовов и сравним с функцией . Из вида функции Аккермана можно сделать вывод, что  изменяется лишь на единицу, либо в большую, либо в меньшую сторону, причём  после достижения некоторого максимума снова принимает значение равное нулю и снова начинает увеличиваться. Рост начинается после того как перестаёт выполняться условие . Этот процесс проиллюстрирован графиком на рисунке 6.

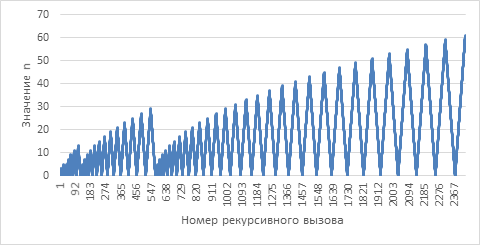
Рисунок 6. Значение аргумента n в зависимости от номера вызова для . Вызовы приведены в хронологическом порядке

А функция  продолжает свой рост на протяжении всех последующих вызовов и значение которое она вернёт будет равно как раз номеру вызова. Из этих соображений видно, что значение  для  будет превышать значение  причём с ростом n разрыв будет увеличиваться всё больше, отсюда можно сделать выводы о более высокой степени роста функции количества вызовов.

Вывод

В результате нашей работы было доказано, что функция Аккермана не является примитивно рекурсивной, было показано как применяют ее на пратике, а также была выведена формула для подсчета рекурсивных вызовов функции Аккермана при различных входных значениях.

Код на языке С

Приложение 1.

long RecursionAckermann (int m, int n)

{

            if (m == 0)

            {

                        return n + 1;

            }

            else if (n == 0 && m > 0)

            {

                        return RecursionAckermann(m - 1, 1);

            }

            else

            {

                        return RecursionAckermann(m - 1, RecursionAckermann(m, n - 1));

            }

}

Приложение 2.

const int tsize = 20000;

int s[tsize];

long IterationAckermann (int m, int n)

{

            int t = 1, d = 1;

            s[t] = m;

            do

            {

                        m = s[t--];

                        if (!m)

                                     n++;

                        else if (!n)

                        {

                                     s[++t] = m - 1;

                                     n = 1;

                        }

                        else

                        {

                                     s[++t] = m - 1;

                                     s[++t] = m;

                                     n -= 1;

                        }

                        if (t > d)

                        {

                                     d = t;

                                     if (d > tsize)

                                                 return -1;

                        }

            }

            while (t);

            return n;

}

Приложение 3.

int ReverseAckermann (int n)

{

            int k = 1;

            int value;

            while(true)

            {

                        value = RecursionAckermann(k, k);

                        if(value >= n)

                                     return k;

                        k++;

            }

}

Приложение 4.

double Hyper (int a, int n, int b)

{

            if (n == 0)

                        return b + 1;

            if (n == 1 && b  == 0)

                        return a;

            if (n == 2 && b == 0)

                        return 0;

            if (n >= 3 && b == 0)

                        return 1;

            if ( n>= 1 && b >= 1 && a >= 0)

                        return Hyper(a, n-1, Hyper(a, n, b - 1));

            return -1;

}