Разработка математической модели процесса закалки и отжига стали

Development of mathematical model of the process of quenching and annealing of steel

Anna Sheveleva

master's student of Lipetsk state technical University, Russia, Lipetsk

Boris Maslov

master's student of Lipetsk state technical University, Russia, Lipetsk

Elena Nemtseva

master's student of Lipetsk state technical University, Russia, Lipetsk

Igor Tsyganov

scientific supervisor candidate of technical Sciences, associate Professor of Lipetsk state technical University, Russia, Lipetsk

Irina Kovalenko

scientific supervisor candidate of technical Sciences, associate Professor of Lipetsk state technical University, Russia, Lipetsk

Аннотация. Разработка режимов закалки стали для улучшения механических, физических и технологических свойств среднеуглеродистых сталей осуществлялась математическим моделированием процессов.

Abstract. The development of steel hardening modes to improve the mechanical, physical and technological properties of medium-carbon steels was carried out by mathematical modeling of processes.

Ключевые слова: сталь, термическая обработка математическая модель, расчет, режим, химический состав, структура, предел прочности, твердость.

Keywords: steel, heat treatment mathematical model, calculation, mode, chemical composition, structure, tensile strength, hardness.

Для решения задачи по разработке математической модели процесса закалки и отжига стали необходимо, прежде всего, её математическое описание с обозначением всех переменных записью уравнений, описывающих протекающие реальные физические процессы, вводятся математические ограничения, задаются начальные и конечные данные. Температуры начала и конца фазовых превращений A₁ и A₃, и S предопределяются содержанием легирующих элементов в среднелегированной стали [1. с. 5‒30].

1. Среднее содержание легирующих элементов (% массы) в среднеуглеродистой среднелегированной стали рассчитывается по формуле

X_j = (Y_j + Z_j)/2,                                                 (1)

где X_j ‒ среднее, Y_j ‒ наименьшее, Z_j ‒ наибольшее.

2. Положение критической точки S в эвтектоиде

                                                        (2)

                                               (3)

                                                        (4)

где S₁ ‒ среднее, S₂ ‒ минимальное, S₃ ‒ максимальное значение.

V_iX_j, V_iY_j, V_iZ_j ‒ функции изменения значения точки S при увеличении легирующих элементов.

3. Температуры начала и конца фазовых превращений A₁ и A₃,

                                                    (5)

                                                   (6)

                                                    (7)

где А₁ ‒ средняя, W₁ ‒ минимальная, D₁ ‒ максимальная температура эвтектоидного превращения, ^oC; F_i, Y_i, P_i ‒ функции изменения положения критических точек A₁, W₁, D₃ при прибавлении легирующего элемента.

                                                    (8)

                                                  (9)

                                                    (10)

где A₃ ‒средняя, W₃-минимальная, D₃-максимальная температура начала превращения, ^oC;

F_j, H_j, P_j ‒ функции, показывающие на сколько изменится положение точек A₃, W₃, D₃ при добавлении легирующего элемента.

4. Температура нагрева под закалку доэвтектоидной стали рассчитывается по формулам

                                                (11)

                                               (12)

                                                (13)

где T₁ ‒ средняя, Т₂ ‒ минимальная, Т₃ ‒ максимальная, ^оС.

5. Температура нагрева под закалку заэвтектоидной стали рассчитывается по формулам

                                                (14)

                                                (15)

                                                (16)

6. Время нагрева под закалку в мин.

а) форма образца ‒ цилиндр

                                                 (17)

где d ‒ диаметр образца, мм;

K₁ ‒ коэффициент среды ( для газа ‒ 2, соли ‒ 1, металла ‒ 0.5);

l ‒ коэффициент распределения деталей в печи;

б) форма образца ‒ параллелепипед

                                              (18)

где С ‒ толщина образца.

7. Время выдержки при температуре закалки, в мин.

                                               (19)

8. Общее время пребывания деталей в печи, в мин.

                                                (20)

9. Определение охлаждающей среды:

а) определение среднего балла зерна

                                         (21)

где Б_min ‒ минимальный,

 Б_max ‒ максимальный балл зерна

б) определение идеального критического диаметра сплава Fe‒C:

                           (45)

в) определение идеального критического диаметра, мм

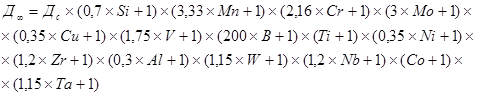      (22)

г) определение критического диаметра закалки, мм

Если Д_¥ < 200, то

1. воздух                                 (23)

2. вязкое масло                        (24)

3. масло                                     (25)

4. вода                                     (26)

5. 5%-ный раствор NaOH       (27)

Если Д_¥ > 200, то

1. воздух                        (28)

2. вязкое масло                           (29)

3. масло                                     (30)

4. вода                                     (31)

5. 5%-ный раствор NaOH                   (32)

д) сравнивая диаметр образца с критическим диаметром закалки Д находим охлаждающую среду.

При Д = d охлаждаем в данной среде.

10. Определение углеродного эквивалента

 (33)

11. Определение необходимости обработки холодом.

а) определение критических точек М_н, М_к, М_с.

Точка М_к определяет необходимую температуру охлаждения;

точка М_н определяет эффект обработки холодом;

точка М_с определяет допустим ли разрыв во времени между закалкой и обработкой холодом.

Определяем точку М_к.

При У_экв < 0,514 обработка холодом не производится, т.к. точка М_к расположена выше комнатной температуры.

При У_экв < 0,86

М_к = 1026 У_экв² + 733 У_экв + 95,7                             (34)

При У_экв > 0.8

М_к = -30,526 У_экв² – 60,227                                      (35)

Определяем точку М_н.

При 0,514 < У_экв < 0,6

М_н =840 У_экв² - 1120 У_экв + 650                                (36)

При У_экв > 0,6

М_н = -45 У_экв + 245                                                   (37)

Определяем точку М_с.

При 0,514 < У_экв < 0,6

М_с = 6071,4 У_экв² + 2610,7 У_экв + 650                      (38)

При У_экв > 0,6

М_с = -225 У_экв – 65                                          (39)

б) определение содержания остаточного аустенита.

      (40)

            (41)

в) содержание А^ост не должно превышать 15‒20 %, а если более то обработка холодом целесообразна

г) определение температуры обработки холодом

                                                   (42)

д) выдержку изделий при обработке холодом считают до момента сквозного их охлаждения из расчета 1,0‒1,5 мин, на каждый мм диаметра или толщины изделия

 мин                                       (43)

е) время охлаждения:

 мин                                    (44)

12. Определение эквидистантной твердости

                        (45)

где НRС_э ‒ твердость после отпуска.

13. Определение температуры нагрева для отпуска при заданном времени выдержки и твердости:

                                                 (46)

где А, С ‒ коэффициенты, зависящие от времени выдержки

Температуру отпуска определяем для двух времен выдержки t_во=1 час, t_во=2 часа по монограмме Гуляева И.П.

для t_во = 1час, t_о = -11,85Н_эк + 149,5                       (47)

для t_во = 2часа, t_о = -17Н_эк + 1016                                     (48)

16. Определение времени нагрева при отпуске:

              (\49)

После математического описания с обозначением всех переменных и записью уравнений, описывающих протекающие реальные физические процессы была составлена блок-схема в виде графического изображения, составленного из отдельных элементов – операционных блоков.

Для разработки режима термической обработки среднеуглеродистых и среднелегированных сталей была разработана программа “TERMOOBRABOTKA”.  При вычислении режима термической обработки компьютер запрашивает следующую информацию:

·          химический состав стали;

·          форму, размер детали (шар, цилиндр, параллепипед) и расположение ее в печи;

·          время выдержки при отпуске, необходимую твердость после отпуска.

После ряда вычислений машина выдает информацию о:

·          времени нагрева, времени выдержки, температуре при закалке;

·          времени нагрева, температуре при отпуске;

·          целесообразности и параметрах обработки холодом.

Для исследования были взяты несколько марок конструкционных сталей [2‒4]. Режим термической обработки, критические точки, твердость, температура закалки и температура отпуска были получены при расчете на ЭВМ и опытным путем сопоставлены между собой. Расчетные и экспериментальные данные различаются не более 7 %.